FARM 4 SECTION 23

Considerable work was done by Lothrop on Farm 4 in Sections 23 & 36. It was a rich field, providing many mounds and a variety of artefacts or monuments.
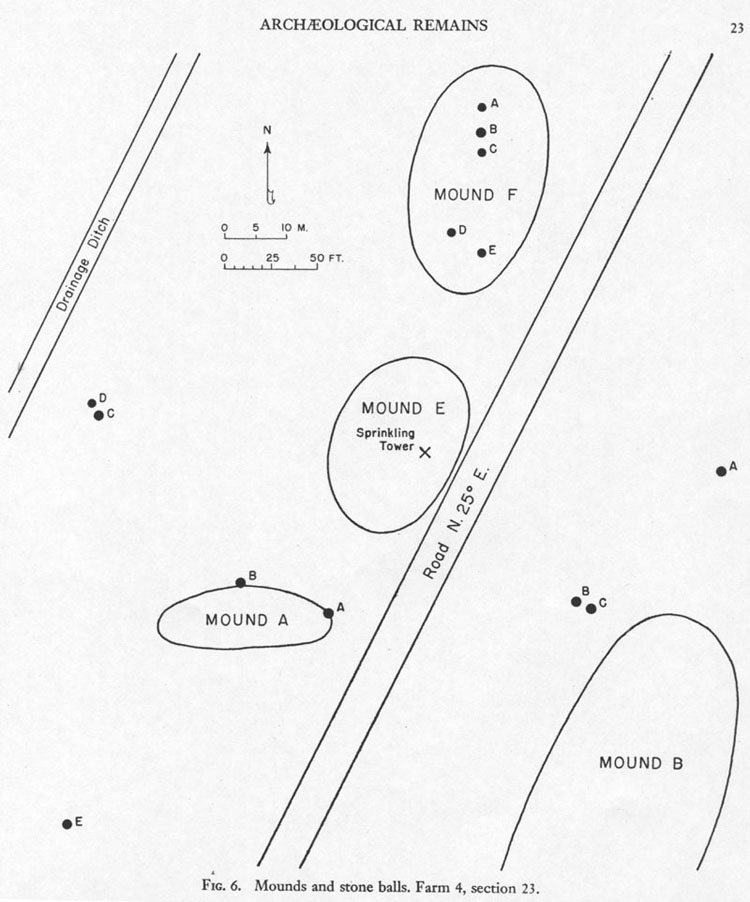
The above scaled map plan shows component stones "in situ" on Mound F and other components that were probably in their original, intended positions when Lothrop surveyed the site in 1948. Stone E at the bottom left was probably a hubstone, from which distance and angle fixes were taken to "outer markers" D & C on that western side of the site. Alternatively, stone A on the extreme centre right of the map plan seems to have been another hubstone for taking distance and angle fixes onto "outer marker" components that sat on Mounds F, E, A & B. The two stones B & C on this eastern side of the site seem also to act as "outer markers" to that hubstone. Stones A & B, which sit to the side of Mound A, probably once sat on the mound itself, but it's very likely that other off-mound stones were "in situ". The following are the distance and angle readings determined in AutoCAD over Lothrop's precisely scaled drawing.
1. Hubstone A (eastern side of the site) to Stone A, Mound F. Distance = 226.8-feet (navigational & lunar code); angle = 145.8-degrees return (navigational & lunar code).
2. Hubstone A (eastern side of the site) to Stone B, Mound F. Distance = 216-feet (lunar code); angle = 324-degrees (navigational & lunar code).
3. Hubstone A (eastern side of the site) to Stone C, Mound F. Distance = 207.36-feet (navigational); angle = 141.75-degrees (dynamic lunar code).
4. Hubstone A (eastern side of the site) to Stone D, Mound F. Distance = 190.08-feet (navigational & lunar code); angle = 130.68-degrees (navigational code).
5. Hubstone A (eastern side of the site) to Stone E, Mound F. Distance = 170.1-feet (lunar code); angle = 311.04-degrees (navigational code).
6. Hubstone A (eastern side of the site) to Stone C. Distance = 99-feet (navigational code); angle = 44.8-degrees return (navigational code).
7. Hubstone A (eastern side of the site) to Stone B. Distance = 102.4-feet (navigational code); angle = 49.5-degrees return (navigational code).
8. Hubstone A (eastern side of the site) to Hubstone E (southwestern side of the site). Distance = 396-feet (Earth diameter & equatorial code); angle = 243-degrees (strong lunar code).
9. Hubstone E (southwestern side of the site) to Stone D (west centre side of site). Distance = 216-feet (strong lunar and Precession of the Equinoxes code); angle = 3.54375-degrees (strong lunar code related to the duration of the lunar year).
10. Hubstone E (southwestern side of the site) to Stone C (west centre side of site). Distance = 210-feet (navigational code); angle = 4.608-degrees (navigational code).
There is much to suggest that Mound E, observed by Lothrop to have a sprinkling tower built atop it (it probably once had an array of statues on it), was used as a crossover point for lines running from hubstone A on the eastern side of the site to stones D & C on the western side. Although the field stones were obscured by the mound sitting centrally, from an observation position on the mound both sets could be seen. This is a very common surveying practice, where a centre ridge between two valleys is used to accurately fix the positions of low lying markers, obscured from view on each side of the ridge. A skyline ridge marker is set up to conspicuously indicate the line connecting the valley markers. This researcher has often found stone ridge markers (ancient surveying trigs) set up like this and has, on occasions, calculated where they should be after finding valley markers ... then located the ridge one using a GPS device.
11. Hubstone A (eastern side of the site) traversing Mound E to stone D on the western side of the site. Distance = 340.2-feet (lunar nutation cycle duration code); angle = 96-degrees return (navigational code).
12. Hubstone A (eastern side of the site) traversing Mound E to stone C on the western side of the site. Distance = 336 -feet (strong navigational code); angle = 275-degrees (navigational code).
All in all several sites of Farm 4, Section 23 seem to be substantially intact and still able to act as sentinels to the codes built into their positions and dimensions. Researchers are encouraged to "test" the numerical values(whole numbers and simple fractions) found to reside in these positions. They work admirably in mathematical progressions to divulge navigational and astronomical-cycle numbers, much used by the ancient cousin European nations.
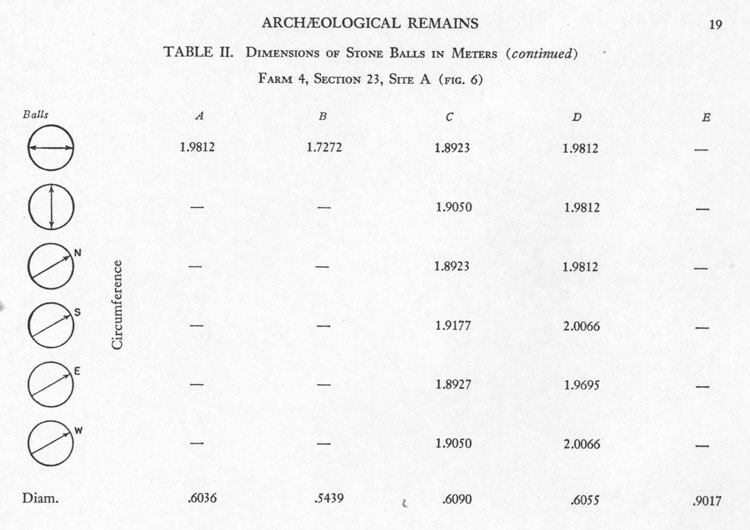
Here is an analysis of the dimensions of individual stone balls found on Farm 4, Section 23.
STONE SPHERE A.
Lothrop gives a circumference of 6.5 feet for this stone. This value would be significant in Calendar calculations, inasmuch as under the Sabbatical Calendar system, used by peasant farmers from the Mediterranean and Europe to the Americas, there were 13-months of 28-days each per year or 52-weeks of 7-days duration each (364-days per annum). This system was allowed to run for 7-years before correction at a festival.

One of the ancient South American Calendar disks. The total number of calibration segments, in 3 concentric rings, is 52 (13 X 4).
It's very likely that this circumference measured by Lothrop was designed to be 78.125-inches, which is only 1/8th of an inch larger than Lothrop's figure. Under such circumstances the circumference would relate to navigation.
STONE SPHERE B
Lothrop measured this circumference at 68-inches, but the true intended value would have been 1/25th of an inch larger or 68.04-inches. This stone ball carried a very important lunar code that related to the 6804-day lunar nutation cycle. The diameter code for this sphere was found by using the rendition of PI @ 3.15. Therefore: 68.04-inches ÷ 3.15 = 21.6. Note: During the Precession of the Equinoxes the Sun spends 2160 years in each House of the Zodiac. Note also that the Moon is 2160-miles in diameter.
STONE SPHERE C
Lothrop measured this stone to be just slightly in excess of 6.2-feet in circumference. This stone coded a quarter of the circumference of the Earth under each of the 3 geodetic or navigational systems in use by the European cousin nations of antiquity . Students of navigation, in measuring this circumference would have realised that it meant (literally and symbolically):
STONE SPHERE D
One of Lothrop's measurements puts the circumference of this stone at the same value as sphere A in the same set, however his largest measurement ranges to 79-inches with an average at 78.32. The intended value was 78.75-inches (6.25 Greek feet), which was the standard code for the diameter of the Earth. Therefore:
Under the first geodetic reading or "6&7" combined family of numbers
Under the second geodetic reading or "11" family of numbers
STONE SPHERE E
Lothrop calculates the diameter of this stone to be 2.9583 feet. The intended code would have been 2.953125-feet or 1/16th of an inch less than Lothrop's estimate. This is a very important lunar code used over several continents. The "inch" value of this diameter is 35.4375 (35 & 7/16ths). Note: The lunar year is 354.375-days and half the base length of the Khafre Pyramid of Egypt is 354.375-feet. This stone's diameter is also the same as the width of the Druidic Calendar of Coligny brass plaque of Ain, France (2.953125-feet or 35.4375-inches). Note: A lunar month is 29.53125-days to a tolerance of under 1-minute.
Using PI @ 22/7 this diameter (35.4375-inches) converts to a circumference of 111.375-inches, which is a very important mnemonic code for remembering the 24750-mile equatorial circumference. In an age where there was heavy reliance on memory and special "trigger" numbers that would help one to learn to interchange navigational numbers with lunar numbers, the following mathematical trick seems to have been applied:
By making a disk with a circuit of 891 inches (which means 2.475 or 2 & 19/40ths inches X 360), then:

Lothrop continues to work on Farm 4, Section 23, but across the road to the East of Site A.
STONE SPHERE A.
Unfortunately, although the remains of Stone Sphere A were there, it had been blasted by local treasure seekers who had heard a rumor that the stones contained gold inside them. A number of stones were destroyed by drilling and blasting to expose their innards. Lothrop makes the following very interesting observation about these stones at site B.
This site lies across the road and to the east of site
A (fig, 6). It consists of a mound and three stone balls. The mound, one of
the largest in the area, still stands about 3 meters (10 feet) high ...
The three stone balls were unique. First, they were made of coquina, a material
seen in no others, either by ourselves or any of the natives we questioned.
Second, all three had a rough spot which evidently once served as a base. As
encountered by us, however, the rough areas pointed upward or sideways (pl.
VII, c), a good indication that they were not in situ but had fallen
from the top of the mound and had rolled or been pushed to their present locations.
Ball A (fig. 6) had been dug out before our arrival and blasted in half in the
belief that it contained gold.

The ball seen centrally is, undoubtedly, one of several in the region that was blasted by treasure seekers looking for gold inside. Its external girth circumference seems sufficiently intact however that we can still extract the dimensional codes built into the stone by the navigator-astronomer artisans who fabricated it. The stone to the far left of the picture resembles a well weathered "coquina" or "concretion" boulder in general appearance. Some of these softer composition limestone-sand or concretion boulders were located by Lothrop as markers in the Diquis Delta of Costa Rica. The round "concretion" boulders were anciently used in New Zealand as markers on hills, in exactly the same way. This occurred before the arrival of the Polynesian-Melanesian Maori, who later annihilated the earlier "Stone builder" civilisation.

1. Archaeologist Ifigenia Quintanilla views one of the Costa Rican stone balls still sitting "in situ". 2. The Park of Spheres in Costa Rica. 3. New Zealand's "ball park" at the Auckland Domain, the regional equivalent to Costa Rica's, some 8,000-miles removed at the other extremity of the Pacific Ocean. Many of our anciently used food plants of New Zealand came by way of South and Central America. The concretion boulders seen in frame 3 were a part of an overland marker system and were removed from their "in situ" position near Silverdale-Orewa to adorn this park in central Auckland. The same migration of markers occurred in Costa Rica (frame 2).
STONE SPHERE B
Lothrop appears to have detected a slight elliptical configuration to the two stones that he measured on this site, so supplies two values, seemingly 90-degrees opposed. The first cross measure he gives as 43-inches. The actual coded measurement would have meant 43.2-inches, which is a dynamic navigational code. Converting this to a circumference using PI @ 22/7ths renders 135 & 27/35ths, which forms a part of a slightly more complex progression to do with the equatorial circumference of the Earth.
In his second cross measure, Lothrop found the stone ball to be something approaching 46-inches in diameter. It's probable intended diameter was 45.8333333-inches, which is a strong navigational code to do with the "11" system of navigation, using the mile of 5280-feet. This diameter converts (using PI @ 3.141818182) to 144-inches circumference, which is essentially a sexigesimal value reducible within a 360-degree environment. Therefore: 144-inches (12-feet) ÷ 360 = .4-inches per degree of arc. This same navigational coding is found within structures from Silbury Hill in Britain to the pre-Maori temple called Miringa te Kakara in New Zealand. To explain:
It's very interesting that these measurements were built into Silbury Hill ... a few thousand years before there was a "Greek civilisation".
STONE SPHERE C
Lothrop's first cross measurement produced a diameter of 4.2-feet or 50.4-inches and this value is both a strong navigational code and lunar code simultaneously. Using PI @ 22/7 produces a circumference of 13.2-feet or 158.4-inches, which is part of a navigational mathematical progression using the "11" family of numbers (mile of 5280-feet).
In Lothrop's other cross-measure of this stone ball (seemingly 90-degrees opposed), the diameter was very close to 4.33-feet. It was, without doubt 3/25ths of an inch less than this in its intended design diameter, as 4.32-feet would be a dynamic and much sought after navigational code. The value would also equate to 51.84-inches. The slope angle of the Great Pyramid is 51.84-degrees.
Using PI @ 3.125 this converts to a (symbolic) circumference code of 162-inches (13.5-feet) and this would be almost an inch short of the true circumference, but still feature as a part of a very important tutorial. Virtually all of the mathematical progressions used by the ancient astronomer-navigators were based upon a "rounded" form of the PHI ratio (1.6180339 to 1) ... rendered as 1.62 (1 & 31/50ths).