CODES OF POSITION FOR KNOWTH'S SATELLITE DORMATORY MOUNDS.

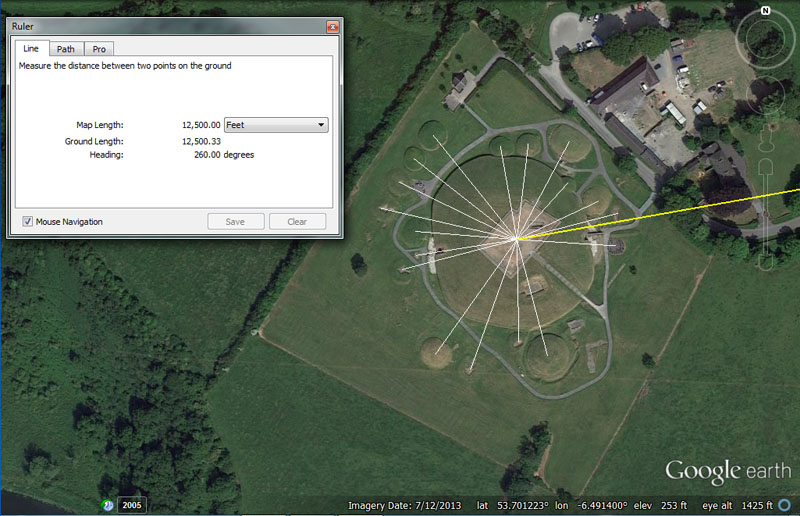
The apparent centre of Knowth chambered mound sits 12500' from the centre of Dowth Henge at 260-degrees azimuth, for a return angle to the henge of 80-degrees.
Both Knowth and Newgrange chambered mounds have undergone very substantial reconstruction or restoration in recent years. It's quite possible that their shapes or apex points, as well as other original coded aspects of their design configurations might be irretrievably lost. It could be expected, for example, that such wide, sweeping summits might have once been adorned with a few marker stones to provide additional distance and angle codes from an observer's position at Dowth Henge.
A large assembly area for tourists now sits atop Knowth Chambered Cairn, affording magnificent views through 360-degrees of vista. From the elevated ground upon which the giant mound was built, Slieve Gullion Mountain in County Armagh should be clearly visible in good weather. The 12500' distance between Knowth and Dowth Henge should have worked very effectively as a surveyor's baseline for calculating the distance to Slieve Gullion using trigonometric mathematics.
Using a very close approximation for the epicentre of the site, lines are seen to emanate out from the apparent middle of Knowth Mound and resolve upon the centres of the circulating satellite mounds. All of these smaller mounds also contained an inner passageway that widened with side alcoves or had side-rooms branching off.
It would appear that each satellite mound was built to be a coded distance and angle out from the epicentre or hub position of the huge Knowth centre-mound. All of these chambered mounds would have acted as both dormitories and code-bearing repository classrooms for students of navigation and astronomy, studying their craft in the Boyne Valley.
Here are the apparent or best-guess distance and angle codes for each satellite mound in relation to the reconstructed centre mound:

Survey lines run from the apparent centre of Knowth Chambered cairn to a selection of chambered satellite mounds, sitting away at precise distances and angles. The vectors seen were generated within AutoCAD computer program. These satellite, dormitory mounds (of which there were once about 37) are not placed haphazardly, but at specific, coded positions and each was a classroom in its own right by way of its purpose-built position or measurable attributes.
Often, with these satellite mounds, the doorways are oriented towards the centre of Knowth chambered cairn, showing an intention to encapsulate the coded angle listed. Here are the best guess, intended codes of position, based upon measurement and angle standards being used in circa 3000 BC and before.
1. The distance is 243' and the return angle, centre-to-centre, back to Knowth chambered cairn was (for tutorial purposes) intended to encode 340.2-degrees.
Both the distance and angle numbers generated are strong lunar coding and, in the 6804-day lunar nutation cycle (where the Moon moves from lunar major standstill to lunar minor standstill and back to lunar major standstill again). There would be 243 Sabbatical Calendar months (of 28-days duration each) in this cycle.
Equally, the intended azimuth angle of 340.2-degrees is in mnemonic reference to 3402-days, the half period of the the 6804-day lunar nutation cycle. The intended diameters of the southern circle at Avebury Henge or the Ring of Brodgar were 340.2' and a circumnavigation of the Khafre Pyramid of Egypt was 34020-inches (708.75' per side).
From this value at Knowth, students would learn an important mathematical progression related to tracking the journey and oscillations of the moon within the 6804-day lunar nutation cycle.
2. The distance was intended to code 177.1875' (177 & 3/16th') and the angle was 177.1875-degrees.
Both the distance and the angle are very strong lunar codes and the duration of 177.1875-days would equate to half a lunar year of 354.375-days.
The Khafre Pyramid of Egypt @ 708.75' in length = 2 X 354.375' or 4 X 177.1875'.
3. The distance is 240' and the angle is 198-degrees from Knowth chambered cairn to the outer satellite mound.
In a number progression the value 240 (2/3rds of 360) generates values much used in readings of the 360-degree compass or, equally, the time measurement system of days, minutes and seconds, attributed to the Sumerians. It is a highly useful and versatile value within ancient calculation systems.
The degree angle coding relates to the diameter of the Earth
@ 7920-miles, of which 198-miles would be 1/40th part. Also, a distance of
198' would be 1/30th of an ancient Scottish mile of 5940' (1920 ancient Scottish
ells of 37.125" each ... 37 & 1/8th").
Under the English mile (5280') or Scottish mile (5940') systems, the increments
of length used were based upon progressions of the value "11" and
the equatorial circumference of the Earth was set at 24750 English miles or
22000 Scottish miles.
4. The distance is 210' and the angle from the satellite mound back to the centre of knowth is 343.75-degrees. The vector appears to go through the doorway entrance into this satellite mound.
A mathematical progression of 21 or 210 would generate many values used in navigation or cyclic astronomy and 210' would equate to 1/25th of the 5250' mile or 1/3rd of a stadia @ 630', etc. There would be 324 intervals of 3-weeks (21-days) in the 6804-day lunar nutation cycle.
The degree angle is navigational coding and the sum of 34.375-miles would be half of 68.75-miles (1-degree of arc in an equatorial circumference of 24750-miles).

5. The distance is 201.6' @ 255.15-degrees.
This distance is in homage to the 6048' in 1-minute of equatorial arc, of which 2016' would be 1/3rd or 201.6' would be 1/30th.
The degree angle is related to the lunisolar Sabbatical Calendar count, where 2551.5-days (7.2 lunar years) were tracked alongside 2556.75-days (7 solar years), so that the position and phases of the moon around the Earth were known daily alongside the position of the Earth around the sun. With this knowledge such things as weather predictions could be made with good relative accuracy, leading to such decisions as when to plant or harvest or predictions about when & where terrible, dangerous storms at sea were likely to occur. The moon and its position around the Earth is the biggest determinant of weather.
6. The distance is 172.8' @ 81-degrees return.
This vector from the centre of Knowth passes through a passage door & window entryway, over the standing "male & female" stones to resolve upon an outer, marker-stone structure.
It would be plausible to assume that the intended code of distance was 172.8', as this is a much used ancient value for navigation and volume measures (a cubic foot is 12" X 12" X 12" = 1728 cubic inches). Likewise, the largest of the Egyptian Royal cubits was 20.736" or 1.728'. Silbury Hill in Southern England and Montfortescue in Meath, Ireland seem to have carried circumference codes of 1728', based upon diameters of 550' (using PI at 1728/550ths).
The degree angle is in homage to the half value of either rounded PHI (1.62 to 1) or pure PHI (1.6180339 to 1), rendered in the enlarged ratio of either 81 or 80.901695. A sound knowledge of the PHI ratio and how to calculate using it was integral to "squaring the circle" for use in volume calculations, etc.
7. The intended codes were probably 175' or 176' @ 275-degrees.
The sum of 175' would be 1/30th of the 5250'-mile and 176' would be 1/30th of the 5280'-mile.
The degree angle also accentuates a much used value in ancient calculations and 2750' would be 1/6th of an ancient English league of 16500'.
8. The distance code is 237.6' @ 283.5-degrees and, once again, the vector skims the door entry into the satellite mound's central chamber.
A distance of 23760' would amount to 4.5-miles of 5280' and, at the same time 1/5500th of the 24750-mile equatorial circumference.
The degree angle is lunar and the Khafre Pyramid of Egypt (a pyramid of the moon) is 2835' in base perimeter. The sum of 2835-days would equate to 8 lunar years. The return angle could also read as the slightly increased code of 103.68-degrees and relate to the speed at which the 24883.2-mile Earth spins in 24-hours (1036.8 MPH).
9. The distance is 225' @ 297-degrees. Again, the vector goes through the doorway of the satellite mound into the inner living quarters.
The 225 value is in homage to the 360-degree compass circle, in which 22.5-degrees is 1/16th part. Also, the sum of 2250-miles would be 1/11th of the 24750-mile equatorial circumference or 22.5' would be 1/28th of a stadia (630') etc.
The degree angle is in homage to the ancient Scottish mile of 5940', the half value of which was 2970'.
10. The distance was probably read as 224' @ 309.375-degrees. The sum of 224' is 1/27th of 1-minute of arc (6048') and the value features prominently in ancient calculations. The weight adopted (from more ancient systems) for the ton weight was 2240 lbs (20 CWT of 112 lbs each).
The sum of 3093.75-miles would be 1/8th of the 24750-mile equatorial circumference or 45-degrees of arc.
11. the distance is 230.4' @ 141.75- degrees return. Again the vector passes perfectly through the doorway into the satellite chambered mound.
If the 25920-year duration of the Precession of the Equinoxes were being tracked or calculated within a 360-degree circle, then each 32nd part (11.25)-degrees would equate to 2304-years. Each of the 30 lintels of the Sarsen Circle of Stonehenge averaged 11.52' (half of 23.04') for an outer rim circuit of 345.6' (In miles, this would be 1/72nd of the 24883.2-mile circumference). The sum of 230.4-miles would be 1/108th of the 24883.2-mile circumference.
The degree angle is lunar coding and there would be 2.5 intervals of 141.75-days in the 354.375-day lunar year. Likewise, there would be 48 intervals of 141.75-days in the 6804-day lunar nutation cycle.
12. The distance is 165' @ 352-degrees.
This distance is in homage to the rod or perch (16.5') or league (16500'). It is also 30 old fathoms of 5.5' each.
The degree angle coding is also navigational under the same "11" measurement standard and 352' would be 1/15th of a 5280'-mile or 64 old fathoms.
13. The distance is 170.1' @ 8.75-degrees.
The distance is lunar coding and 1701-days would be 1/4th of the 6804-day lunar nutation cycle. This distance would also be the radius of both the southern circle at Avebury Henge and the Ring of Brodgar. The vector, once again, passes directly through the doorway into the chambered mound.

14. The distance is 198' @ 29.53125-degrees (29 & 17/32nds). Again, the importance of this dynamic angle code is attested to by the fact that the vector passes through the large door, deliberately orientated to preserve this special scientific number.
A distance of 198' is navigational and 1980-miles would be 1/4th of the diameter of the Earth or half its radius. Also, 198-miles would be 1/125th of the 24750-mile equatorial circumference.
The degree angle is, of course, in homage to the lunar month, correct to within a minute of time. One way that ancient astronomer-mathematicians used to calculate this number was 1890 ÷ 64, as decipherable from the Druidic, Calendar of Coligny brass plaque artefact of France.
15. The distance code is 136.08' @ 43.2-degrees.
The distance code is in homage to the 6804-day lunar nutation cycle in which 1360.8-days would be 1/5th part.
The degree angle accentuates the multi-use number 432, used in many kinds of ancient calculations, both lunar and navigational. The 6804-day lunar nutation cycle is 15.75 intervals of 432-days (10368-hours). The sum of 432' would be 1/14th of 1-minute of arc (6048').
16. The distance is 162' @ 65.34-degrees.
This distance is in homage to "rounded PHI" (1.62) or the pure PHI (1.6180339) ratio, both values of which were highly important to ancient calculations, whether lunar, navigational or in terms of assays (especially volumes).
The degree angle is navigational and 65340' would be 1/2000th of the 24750-mile (of 5280') equatorial circumference.
17. The distance is 186.624' (186 & 78/125ths) @ 75.6-degrees.
This distance is navigational coding and 186624' would equal 1/700th of the 24883.2-mile (of 5250') equatorial circumference. Likewise, 1 & 1/3rd X 18662.4-miles = 24883.2-miles.
The degree angle is navigational, as well as lunar and 756' (the length of the Great Pyramid) is 1/8th of 1-minute of equatorial arc (6048'). At the same time, the 6804-day lunar nutation cycle is 9 X 756-days.
18. The distance and angle to the centre of the post circle seems to be coded to achieve 176' @ 93.312-degrees. Like other post circles in England or North America it was undoubtedly designed to teach distance and angle codes in miniature (micro learning environment) before novices ventured out into the wider landscape (macro learning environment) to work with the numbers in navigational exercises. It's probable that children received rudimentary tutorials in these post circles and were very conversant with the scientific numbers by the time they were teenagers, just as modern children become very adept in their knowledge of computers.
This distance is, of course, 1/30th of a mile and 1760-yards (of 3' each) = 5280'.
The degree angle encodes a much used value of antiquity that found its way into the weights and measures standards of several civilisations. For example, the Sumerian / Babylonian heavy Talent was 933120-grains. The sum of 933120' would be 1/140th of the 24883.2-mile (130636800') equatorial circumference of the Earth.
OVERLAND NAVIGATION USING THE CELTIC CROSS.
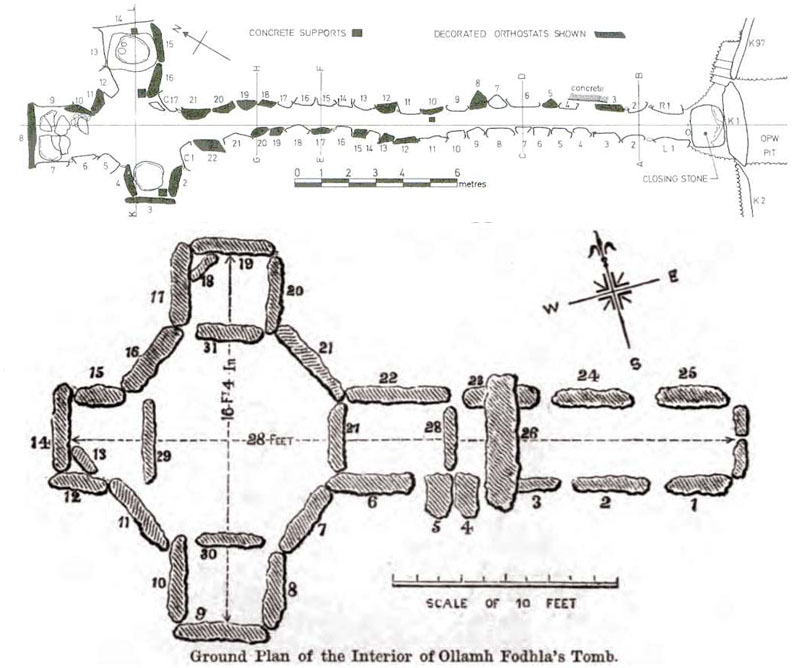
The interior designs of the so-called passage tombs of Knowth, Newgrange and Loughcrew, etc., are essentially in the shape of a Celtic Cross, which demonstrates that this cruciform style was highly revered in the 4th millennium BC and an integral part of the culture. At Loughcrew in particular (bottom picture), students in the main circle chamber could receive instruction on how the design configuration worked as a navigational aid in overland journeys. The illumination of these passages by the Sun on certain, highly-significant days was symbolic of the Sun & Cross conjoined as one.
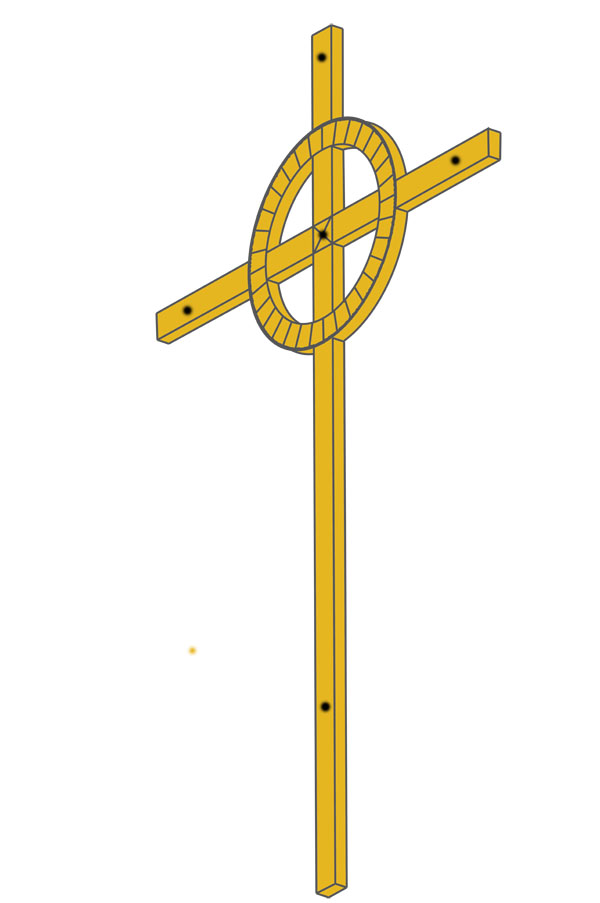
The Celtic Cross shown was scaled in AutoCAD to be 31.5" tall or 1/4th of a reed of 10.5'. At this length and with calibration marks at the rear, a seasoned astronomer-navigator would be able to do many calculations, including everything essential to tracking the daily sun and moon positions within the lunisolar, Sabbatical Calendar.
All other design features of the above cross, configured within the very exacting environment of AutoCAD, are similarly code-bearing, so that all lengths, breadths, circle diameters (ID & OD), as well as circumferences, could be used for mnemonic recall of calculation principles.
Anyone carrying this relatively small and lightweight cross as a navigational aid would also be able to do the following:
1. If you are lost, confused or off course, find a piece of bare, flat ground that is free of rocks or other surface debris.
2. Stand the cross vertically upright and solidly into the ground, facing the rising sun, then look at the shadow cast by the centre pole of the cross. Insert a fine peg or nail accurately into the ground at the edge of the shadow cast from the top of the cross.
3. About 10 to 15-minutes after putting the first nail into the ground, place yet another nail accurately at the point the shadow has moved to as the sun rose and the shadow shortened.
4. Repeat this process at about 10 - 15 minute intervals until there are 4 or more nails forming a straight line across the ground.
5. The first nail placed marks due West and the last nail placed marks due East.
6. Now remove the Celtic cross from its firmly affixed, vertical position and lie it down on the ground, with the cross arms touching the straight line of nails.
7. Using more nails, pin the cross to the ground so that it can't move.
8. The circle on the cross is divided into 32 sections and, on the outer rim of the circle are 360 knops* or calibrations.
9. The top of the cross now faces due North and the foot of the cross faces due South, with the left cross arm facing West and the right cross arm facing East.
10. Now place a nail with a string attached to it into a pre-drilled hole at the very centre of the circle.
11. One member of the orienteering team lies down to sight from the centre, while another team member walks out in the direction of a known landmark and pulls the string taut and straight. The observer at the cross then directs the string bearer to move left or right until the landmark target is perfectly centred. By reference to where the taut string passes over a knop calibration marker at the edge of the circle, the degree angle to the landmark can be read with excellent relative accuracy.
*Footnote: Knops are the small, raised relief, round button or dot objects that one traditionally finds adorning Celtic Crosses. They were widely used from the ancient Middle East to Ireland and the Brasen Sea of the Temple of Solomon had 600 knops, in two rows, under the brim for counts and calculations.

Left: On the Hill of Tara, incised into stone are these cross-within-a-circle designs which, undoubtedly, date to the fourth millennium BC. Similar incising is found at Loughcrew and, by the 1st millennium BC at least, this "sun-cross" symbol was attributed to the solar god & god of thunder and lightening, Taranis. This god was worshipped in Gaul, Britain and Ireland, as elsewhere, and in the Irish language the word Tarann means thunder.
The large cross-within-a-circle shown to the bottom left, with degree angle vectors flaring out from each quarter, and an ever-increasing outwards spiral beyond that, is very suggestive of a circuitous journey, using the sun-cross for precise degree angle orientation onto horizon targets for navigation.
Right: Dowth chambered mound contains a solar-cross pictogram very similar to the one on the Hill of Tara.
The Celtic cross, which is very sword-like in its design configuration, could well have been used for defence as a pointed wooden spike or sword. During the bronze age, some pointed and sharpened blade examples might have been fabricated for the dual purpose of navigation and as weapons for security. Wolf packs roamed Ireland until late mediaeval times and there were plenty of bears and tusked wild boars for wayfarers to encounter and contend with, well into the AD era.