THE FINAL SECTION OF THIS SITE ... WITH MANY MORE SITES AT NAZCA TO GO.
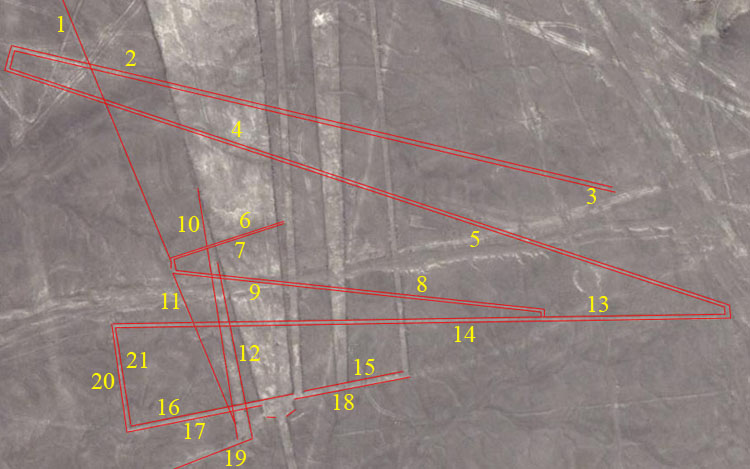
1.The distance is 960-feet and the angle is 157.5-degrees.
A mathematical progression based upon 96 was highly important to navigation and produced values that were applicable to both the Great Pyramid's literal geodetic system, as well as to the mile of 5280-feet. The progression goes: 96, 192, 288, 384, 480, 576, 672, 768, 864, 960, 1056, 1152, 1248, 1344, 1440, 1536, ... 1728, ... 2016, 2112, ... 2304, 2400, ... 2592, 2688, ... 2880, ... 3072, ... 3168, ... 3360, ... 3456, ... 4320, ... 5184, 5280, etc.
The degree angle is providing a progression that codes the Greek mile (5250-feet) and stadia (630-feet) and 157.5-feet would be 1/4th of a stadia.
2. The distance is 1320-feet and the angle is slightly in error at 283.25-degrees (283.5 was the intended target).
The sum of 1320-feet equates to 1/4th of a mile.
The degree angle is very slightly askew by 1/4th of 1-degree and should be based upon the strong lunar code 283.5.
3. The codes for this line appear to be the same as its line opposite (2).
It's very probable that there would have been a station to mark a distance of 1312.5-feet, which value was highly important to navigation.
4. The distance is 1620-feet and the angle is slightly in error at 288.2-degrees (288 was the intended target).
The distance of 1620-feet represents a "rounded PHI" code and the correct rendition of Professor Alexander Thom's "Megalithic Yard" was, undoubtedly, 2 X 1.62-feet or 32.4-inches. This would also have been the value of the original "Vara" of ancient Spain, which is still used in Peru at the slightly drifted measurement of 32.91-inches (an increase of about half an inch). In Northern India, home to the ancient Aryans, a measurement called the Gaz survives, which closely parallels both the Vara and Megalithic Yard.
The 288 value is dynamic and occurs on many ancient sites. The Aubrey Circle at Stonehenge is 288-feet wide each face of the Great Pyramid covers 8-pyramid acres of 28800-square feet each.
5. The distance is 161.8034-feet and the angle remains 288.2-degrees.
Whereas the opposite line coded 1620-feet, this one was, undoubtedly, shorter by 1.66-feet to code 1618.34, or the pure PHI rendition at increased value (the pure PHI ratio is 1 part to 1.6180339 parts. This value was absolutely imperative to ancient European civilisations and all of the volume vessels used by the cousin nations for selling goods at the marketplace had to be based upon the PHI formula in order to ensure correct internal quantities. For example: The formula for fabricating an ancient British Bushel of 2160-cubic inches was: 10-inches ÷ 1.6180339 = 6.180339-inches. This measurement was tripled to be 18.541-inches. A round base of wood was then made to this diameter and vertical sides were then attached that stood 8-inches above the floor of the tub. Because PHI was used to form the base circle, it equated to exactly 270-square inches ... X 8-inches of height = 2160-cubic inches (2160 is a strong lunar or Precession of the Equinoxes code). The Sumerian/ Babylonian Homer volume was 21600-cubic inches or 10 British Bushels.
6. The distance is 256-feet and the angle is 252-degrees.
The 256 value is navigational, but can be used as a ratio for turning the Great Pyramid equatorial circumference figure (24883.2 Greek miles or 130636800 standard feet into Roman or lunar values. Thus 130636800 ÷ 256 = 510300. The lunar period of the moon within the Sabbatical Calendar is 2551.5-days and the sum of 510.3-days would be 1/5th of that period. The method of using numbers from a 256 progression against the known value for the equatorial circumference was probably a mnemonic device for triggering remembrance of the lunar numbers.
The angle is 252-degrees. The Great Pyramid is 756-feet long or 252 X 3.
7. The distance is 247.5-feet and the angle remains 252-degrees.
The length is in homage to the "11" family 24750-mile equatorial circumference.
8. The distance is 792-feet and the angle is 96-degrees.
The diameter of the Earth is 7920-miles.
The value 96 is the basis of a dynamic navigational progression.
9. The coding on this side of the line remains the same as its opposite.
10. the distance is 544.32-feet and the angle is 171-degrees.
The 544.32 code is lunar and there would be 125 periods of 54.432-days in the 6804-day lunar nutation cycle.
Although the 171 value crops up in the parcel of ancient codes, it remains obscure, One of the Station Stones at Stonehenge sits at 342-degrees azimuth from site centre (171 X 2).
11. The length is 345.6-feet and the angle is 337.5-degrees.
The length value is a dynamic navigational number and the outer rim of the Sarsen circle at Stonehenge had a design circumference of 345.6-feet. A mathematical progression based upon this value goes: 345.6, 691.2, 1036.8, 1382.4, 1728, 2073.6, ... 3110.4, ... 5184, ... 9331.2, ... 24883.2. This progression was packed with scientific information, for example: If the Earth is considered to be 24883.2-miles in circumference and completes a full rotation once every 24-hours, then its speed of rotation is 1036.8-MPH. The Stirling Jug of Scotland has a cubic capacity of 103.68-inches, which is the same capacity as the ancient Hebrew Jerusalem liquid standard "Cab", whereas their "Hin" was 311.04-cubic inches. Also, the Great Pyramid @ 756-feet per side equates to 72 Hebrew Reed of 10.5-feet per side. Therefore 72 X 72 = 5184. The slope angle of the Great Pyramid is 51.84-degrees. The Precession of the Equinoxes endures for 25920-years and 1/5th of that period is 5184-years. An ancient British league of 16500-feet, used as a diameter of a circle, creates a circumference of 51840-feet using an ancient rendition of PI @ 3.141818182 (314 & 2/11ths ÷ 100).
The angle codes both lunar and navigational values simultaneously.
12. The distance is 384-feet and the angle is 168.75-degrees.
The 384-feet length is navigational and a circle enclosing Stonehenge's embankments (protruding Avenue excluded) would be 384-feet in diameter.
The degree angle is dynamic and occurs frequently at Nazca. Its coding is lunar.
13. The overall distance, combining both sides of the central branching intersection is 1312.5-feet and the angle is 89.1-degrees
The 13125 value is navigational coding.
The 89.1 value is also navigational coding.
The length coded into the western side was 921.6-feet to a station on the branching intersection that extended north from this line. The 921.6 value was dynamic and the sum of 921.6-miles would be 1/27th of the 24883.3-mile circumference.
The length coded into the eastern side is 388.8-feet from a station on the branching intersection. This is navigational coding and a progression based upon this value goes: 388.8, 777.6, 1166.4, 1555.2, 1944, 2332.8, 2721.6, 3110.4 (note: the 24883.2-mile circumference ÷ 8 = 3110.4-miles).
14. The coded distance remains 1312.5-feet, as does the angle @ 89.1-degrees.
The angle of 89.1-degrees is navigational.
15. The distance is 216-feet and the angle is 78.75-degrees.
The code built into the length is Precessional and lunar.
The code built into the angle is also lunar, but provides the values that occur in Greek lengths.
16. The length is 354.375-feet and the angle remains 78.75-degrees.
The length is, of course, coding the lunar year.
17. The length is 295.3125-feet and the angle remains 78.75-degrees.
The distance is, of course, coding the duration of the lunar month @ 29.53125-days.
18. The distance is 252-feet and the angle remains 78.75-degrees.
The Great Pyramid is 756-feet long and this equates to 252 X 3. This value at Nazca would be 1/24th of 1-minute of arc according to the Great Pyramid's literal reading of the Earth's equatorial circumference.
19. This is the beginning of a long line that stretches for 4725-feet at angle of 68.75-degrees.
The 4725-feet coding is lunar and the design height of the Khafre Pyramid was 472.5-feet. If one divides the 756-feet length of the Great Pyramid by 16 the result is 47.25-feet. If one divides the 708.75-feet length of the Khafre Pyramid by 15 the result is 47.25-feet.
The degree angle is in homage to 1-degree of equatorial arc (68.75-miles) under the "11" family reading of the Earth's circumference @ 24750 British miles.
20. The distance is 234.375-feet and the angle is 352-degrees.
This is a slightly more obscure interim value that works in navigational calculations. For example: The equatorial circumference of the Earth @ 24750 ÷ 234.375 = 105.6. Two British miles equal 10560-feet.
The degree angle is in homage to the mile of 5280-feet and 352-feet would be 1/15th of a mile.
21. The distance is 210 and the angle remains 352-degrees.
The 210-feet value is merely coding a progression based upon 7. Several ancient cubits were 21-inches.
HOW DID ANCIENT EUROPEAN-CAUCASOID PEOPLE FIRST CONCEIVE OF AND CONSTRUCT THEIR PARCEL OF SACRED NUMBERS USED IN NAVIGATION AND FOR MONITORING THE CYCLES? ... "The numbers of civilisation".
As it turns out it was all (or for the mostpart) based upon PHI, the amazing formula or ratio of 1.6180339 to 1.
The ancient cousin nations needed an integrated parcel of numbers that they could apply to navigational methods, the solar count, the lunar count, a lunisolar calendar, weights, measures, volumes and area standards, etc.
They found that the unresolvable ratio PHI could provide them with the dynamic and versatile values they needed for universal application, but the pure PHI formula was difficult to work with and needed to be very slightly "rounded" in order to tame it. They rounded PHI to 1.62 from 1.6180339, which was a variation of only .0019661 or about 2/1000ths. Now they had a very close proximity value that could provide the much sought after mathematical progressions of civilisation. The bulk of the very important progressions were produced by taking numbers from 1 to 18 and multiplying them by 1.62 to get larger or smaller expressions. For example:
1 X 1.62 = 1.62 and a mathematical progression based on this goes: 1.62, 3.24, 4.86, 6.48, 8.1, 9.72, 11.34, 12.96, 14.58, 16.2, 178.2, 19.44, 21.06, 22.68, 24.3, 25.92, 27.54, 29.16, 30.78, 32.4, 34.02, 35.64, 37.26, 38.88, 40.5, 42.12, 43.74, 45.36, 46.98, 48.6, 50.22, 51.84, 53.46, 55.08, 56.7, etc.
One could go to any of the values in this lineup and start an alternative progression. Some root numbers were particularly valuable for navigation and others for the cycles of the moon, etc. Values extending from the above lineup were used to fabricate the measurements of antiquity.
PHI was the "glue" that cemented the number families together and allowed them to work fluidly as one.
An associated method also included simply forming progressions on whole numbers from 2 to 18.
The values to be found on the more ancient quippu string knot calculators, which dealt specifically with the sciences and not with such mundane activities as inventories, will reflect the values seen above or extensions to them. Some quippus of Peru date to at least 3000 BC.
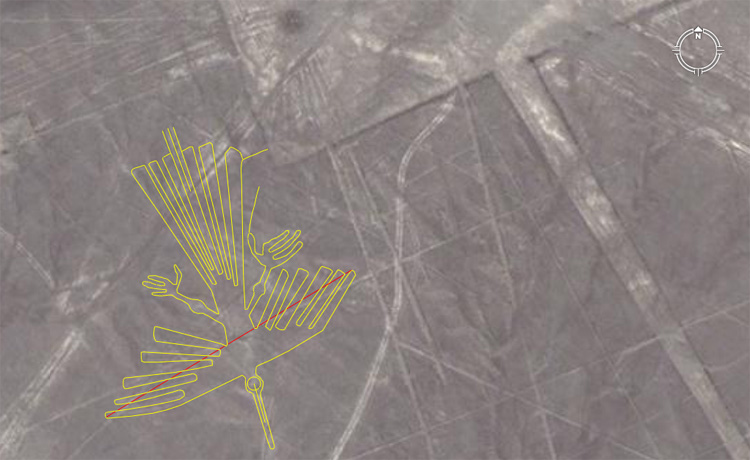
The Condor at Nazca wings it's way across the desert
at an azimuth angle around from north of 161.8-degrees.
This is the angle from the middle of the long tail plume to the centre of
the beak and the Condor is, thereby, coding PHI
in its heading or flightpath. The overall design length of the great bird
is 453.6-feet, or the vertical height of the
Great Pyramid to the top of its flat altar floor. This coding is navigational
and a part of the Great Pyramid's mnemonic formula for working out and remembering
the equatorial circumference of the world.
The wingtip to wingtip code appears to have been 384-feet,
which is also navigational. A circle of 384-feet would perfectly contain the
Stonehenge observatory of Southern England from north to south, with exception
to the Avenue, which juts out beyond the rest of the site at 45-degrees.
The Condor's wingtip to wingtip angle is 59.0625-degrees,
which is a lunar code found on the Khafre Pyramid of Egypt. This is a very
wise old bird, with much to tell apprentices of navigation or students of
astronomy.
"DO IT YOURSELF" ARCHAEOLOGY AT NAZCA.
You're never going to get any sense out of the "so-called" experts and you'll never see any kind of paradigm-shift come about because of them. In short, if you really want to know all that Nazca is, you'll have to tackle the geometry yourself, line by line. Thankfully, sophisticated tools now exist to aid you in this quest. Here's what you need: