The Great Pyramid part 1

The Waitapu standing stone circle in Northland, New Zealand was still being used up until recent centuries and remains reasonably complete in terms of its components and geometric layout. Evidence would suggest that the site was deliberately desecrated as a number of otherwise stable, squat stones, with wide flat bases, lie forlornly on their sides as if deliberately tipped. The wrecked site has, in more recent times, been the catalyst for deep investigation into the purposes of stone circle sites worldwide and the information derived from it has led to an understanding of mathematical concepts inherent in the universal distribution of standing stone circles. By subjecting the surveyed positions of component parts of the Waitapu standing stone observatory to careful computer analysis, an intriguing body of astronomical/ mathematical information has emerged.
From rudimentary beginnings, coupled with ongoing comparative analysis of carefully surveyed site plans, related to the more famous stone circles of Britain, many additional truths have been restored, after lying dormant for centuries or millennia.

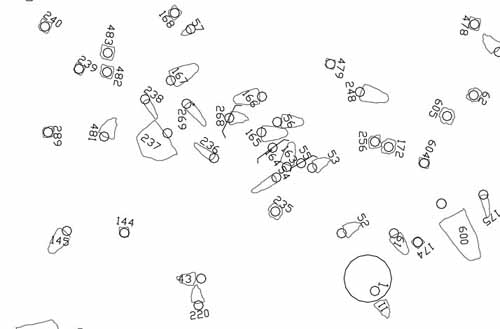
Figure 1: A small section of the Waitapu stone circle observatory from the survey done by the author in 1997. This complex site had sufficient components left to indicate the original geometry from which it was conceived. The stone components, although tumbled, lie very close to their former standing positions and the site has been a veritable "Rosetta Stone" in providing glimpses and clues related to ancient astronomical and geodetic endeavour.

A competent assessment can now be presented on the purposes of the Giza Pyramids, as well as Stonehenge and mathematically proven beyond any reasonable doubt. This will be an intensely involved exercise, requiring the dedicated concentration of the reader. The mathematical concepts are not difficult and are within the capacity of elementary or high school students to grasp.
For those who hate numbers, you are encouraged to participate anyway. Please don't be put off by long tails of decimals...they're harmless enough. Once you get into this exercise you'll find it's fun and the bonus is that at the end of it all you'll understand what our ancient forebears were doing by building pyramids or standing stone circle sites. You'll also have the base formulas you need to tackle standing stone circle sites in Britain, the Mediterranean Continental Europe and North America, sufficient to extract their coded information and decipher them mathematically.
There is, unfortunately, no way of understanding the universal preoccupation of erecting standing stone circles at any conceivable, superficial and non-mathematical level. The ancient astronomers required specific information for the benefit of their populations and standing stone observatories provided that precious information. The sites measured the cyclic paths of celestial bodies and the durations of those cycles, leading to decision making related to such mundane terrestrial events as planting, harvesting or when to schedule the upcoming Maypole festival. They also needed to remember the size of the Earth and that enduring piece of information was, more often than not, encoded into the structures of antiquity The mathematical concepts found on the more complex sites such as the pyramids or Stonehenge indicate deep-set scientific understandings that will both astound and amaze.

There was one major set of coded numbers, which were utilised in many climes and latitudes of the globe. Their point of origin appears to be Egypt and a second region where they are clearly and precisely found is in Britain. The astronomical/ mathematical concepts and measurement standards of the Giza Plateau are so conspicuously displayed on British circle sites, as to leave little doubt that the builders of Stonehenge and other monuments of the British Isles came originally from Egypt. The same astronomical methods found their way to New Zealand at the very 'ends of the Earth', either by a direct migration from Egypt or via Britain as an interim stepping stone to the South Pacific.
It is suspected that Britain itself was the most direct resource of ancient peoples who erected the megalithic structures of New Zealand, inasmuch as no other single region, apart from Britain/ France, duplicated, to the same concentrated degree, the types of specific structures found at the sub-tropical base of the South Pacific.

THE MEASUREMENT STANDARDS USED IN ANTIQUITY BETWEEN EGYPT, GREAT BRITAIN AND NEW ZEALAND.

This very point is the key to unlocking the long-held secrets of structures worldwide and the researcher is encouraged to test the following standards on the sites located in their countries, including North America.
To the great surprise of some, it will be found that the British Standard of measurement is not a recent innovation after all and is, in fact, steeped in age.
Clues that this might be the case have been emerging over recent years, spurred along by such excellent trigonometric surveying work as that of David Wood and his team at Rennes le Chateau in Southern France.
David was able to prove, definitively, by precisely located and distant, overland positions of standing stone markers that the Celtic cubit, as he dubbed it, was 18 British Standard inches.
He also found precise expressions of the British Standard mile of 5280 feet. The structures of the Rennes Valley of the Languedoc Province, are known to be of very remote age.

Although some classicist historians still adhere to the untruth that the British foot measurement originated with Henry the 8th, there is much earlier historical reference to it around the time of the Magna Carta (1215 AD). It was restored, at that time, under a Royal Ordinance entitled, Assize of Weights and Measures, because of problems related to transactions and "short measures" in the market places.
By comparative analysis of standards utilised by Sumerian, Babylonian, Greek and other great civilisations, it can be seen that their systems of weights, measures, volumes, time or degree angle computations, came originally from a universal standard found on the Giza Plateau of Egypt. This will be shown, mathematically, in the dimensions and angles of the Great Pyramid as we proceed. The attributes and similarities between traditional measurement standards of British, Mediterranean Near and Far Eastern peoples, also attest to the very ancient pedigree of the British system.

It must be noted that the concept of breaking a circle into 360 or 720 divisions is also very ancient and our present system of degrees, minutes and seconds of arc has a direct link back to the Near & Far Eastern roots. This truth will be supported by the decipherable geodetic systems encrypted into the Great Pyramid. The Greek astronomer/ mathematician, Ptolemy (circa AD 140) was working to degree accuracies of 1/3600th of arc in 180 degrees when he wrote his 13 volume, Almagest. The Greeks had adopted the ancient Babylonian system of circle calibration.

The sexagesimal chronology systems that we have used since time immemorial are equally ancient. The concept of 24 hours to describe the duration of 1 day, then breaking the hour down in divisions of 60 minutes or 3600 seconds, also stems from the Babylonian and Sumerian "6" based systems. Here are the linear measurements used universally around the ancient world by peoples, originally, of Indo European descent then disseminated to and adopted by other groups as well:

THE SEXAGESIMAL MEASUREMENTS: