From a low, central viewing position the circumnavigating embankment represented a "false or artificial horizon" and was created specifically for marking the alighting positions of stars and planets. No such determinations were possible unless the descending stars were alighting into a pre-built, calculating matrix, where specific degree angles had been pre-set by the positions of component stone and post markers.
The system worked like this:
Say for example the Stonehenge
astronomers wished to fix onto the exact alighting position of Aldebaran,
the bright star in the Hyades (Taurus Constellation), on the night of 1/1/2400BC
when it set very close to, but short of, due west
An astronomer would take up a position at site centre, where a clear view onto
the alighting star was (seemingly) possible between the western standing stones
(now ruined) of the Sarsen circle.
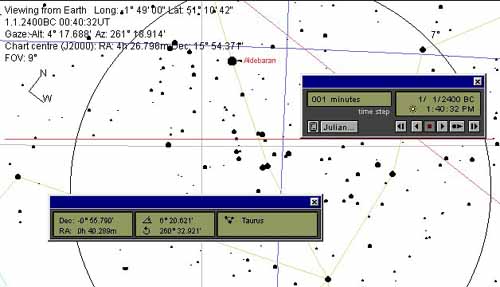
Figure 40: The star Aldebaran descending upon Stonehenge's embankment for the date of 1/1/2400 BC. It is assumed, for the purposes of this demonstration. that an observer, situated at site centre, could watch Aldebaran alight upon the embankment… in a clear view between the standing megaliths of the Sarsen Circle. The red horizontal line represents the approximate level of the embankment artificial horizon. The final landing position would have been very close to 262-degrees.
The astronomer situated at site centre, made his/ her observation from a rigidly
fixed position, where the eye would not waiver from side to side or up and down.
An eyelet sight, probably shaped like the Egyptian Ankh, was slotted into a
precisely positioned plane table (set by a plumb-bob onto a ground marker peg
& to a standard, angled height orientating slightly upward to the crest of the
embankment). The observer could view through this "Ankh" eyelet to the alighting
position of Aldebaran.
Alternatively, one could slot a swivelling alidade (sighting ruler) into the plane
table's centre hole and view along its straight edge to the alighting position of the
star.
Based upon artefacts recovered from Bush Barrow tumulus mound near
Stonehenge, the plane table and alidade method appears to have been used at
the observatory. Professor John North comments, 'Fragments of wood that
the excavators had thought were the remains of a shield were now
described as the remains of an alidade (a sighting rule) and wooden
drawing board or plane table' (see Stonehenge, Neolithic Man and the
Cosmos, page 508).
There would be a standard, upward angle from the fixed sighting position to the artificial horizon and this angle would not vary through 360-degrees of potential observation. It is assumed that the chosen angle would place the alighting position of the target star sufficiently above the thickened horizon atmosphere to eliminate positional distortion caused by parallax (a bending and magnifying effect that gives a false reading as to the exact position of an object hovering near the level horizon).
Working in conjunction with the observer at site centre would be a second
individual, situated at the rear or outer face of the embankment. It would be the
task of this individual to place a manageably sized, pointed marker stone onto
the top of the embankment…as per the "left or right" instructions issuing forth
from the centrally located observer.
Finally, Aldebaran would be made to alight onto the precisely positioned stone or
chalk marker and further calculation work could now be postponed until the next
morning when the sun rose.
After dawn a series of ropes or strings would be pulled out across the
Stonehenge site, which would finally form a giant 3,4,5 triangle. The triangle
would be formed by post-markers (primarily on the Aubrey Circle) that were
preset when the observatory was first built. The 3,4,5 triangle used to calculate
Alderbaran's nocturnal position, for the night previous, would be one that came
very close or the closest to the star's alighting position.
This is how it looked:
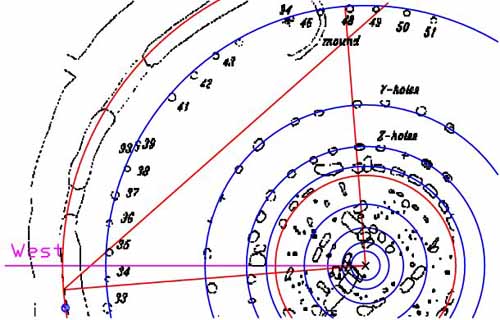
Figure 41: The post positions of the Aubrey circle were set out to be 3,4,5 triangulation stations and a giant 3,4,5 measuring 126 feet (adjacent), 168 feet (opposite) and 210 feet (hypotenuse) was used. This 3,4,5 triangle swivelled through 360-degrees of arc and was fixed to site centre at the 90-degree intersection of adjacent and opposite. The intersection of adjacent and hypotenuse had rope extensions, which ran all the way to the sides of posts on the Aubrey Circle (in this case post 48 for the adjacent and post 49 for the hypotenuse). Alternatively, the opposite ran past post-positions on "Z" or "Y" Holes, before brushing the side of a post on the Aubrey Circle (post 34). It intersected with the hypotenuse, which ran to the side of post 35. That point of intersection (opposite and hypotenuse) was beyond the Aubrey Circle on the embankment (at a point exactly 168 feet from site centre). This was the circle line (embankment) where the observable setting of stars and planets were periodically marked by manually positioned stones (as determined by careful observation from site centre).
It will be noted that a blue dot sits on the embankment circle (red) just below the intersection of opposite and hypotenuse. This is the estimated alighting position of Aldebaran on the night of 1/1/2400 BC...so how do we very accurately determine its exact degree angle by utilisation of this static, inbuilt 3,4,5 triangle (made from ropes drawn to the sides of carefully positioned posts)?
Each of the multiple, pre-built 3,4,5 triangulation positions were at known degree angles. All the astronomer/ mathematicians had to do is choose one at close proximity to the star alighting position, then measure how far the star marker sat from the known angle.
The embankment circle was fashioned to be 1056 feet in circumference (528 feet X 2...336 feet in diameter X PI). This means that every 35.2 inches represented 1-degree of arc or every 17.6 inches was ˝ a degree of arc. Remember, the 176 number was integral to geodetic, earth navigational determinations (the altar atop the Great Pyramid was 44 feet per side or 176 feet for the whole perimeter...there are 1760 yards in a mile...1/8th of 35.2 inches is 4.4 inches...there are 2880 increments of 4.4 inches in 1056 feet, etc.).
One geodetic circle in use at Miringa te Kakara's Crosshouse in New Zealand was based upon a circumference of 176 feet (56 feet X PI…marginally rounded). This put the ratio of the Crosshouse's intended 176 feet circle (1/30th of a mile) @ 1:6 of the Stonehenge embankment circle. The full circumference of the embankment circle (1056 feet) was exactly 1/5th of a mile.
Although there are slight discrepancies to be found in individual sections of Stonehenge's Aubrey Circle, the distance between one 3,4,5 triangle station and another next to it, was, generally, set to a 6.4-degree spacing. On the Aubrey Circle, that translated fluidly to every 16 feet.
There were two swivelling sets of 3,4,5 triangles configured as mirror images of each other. Both could run either anti-clockwise or clockwise. There are some areas of the site where the distance between Aubrey stations exceeds 6.4- degrees and the reader is encouraged to experiment with the following ANIMATED DRAWINGS to see the multiples of 3,4,5 triangulation possibilities. There are simply too many to show them statically within this limited article.
Figure 42: By clicking the mouse on the picture, the reader will be able to move this red 3,4,5 triangle to any desired position around the Aubrey Circle. Remember that the ancient astronomers were using ropes, running to the sides of Aubrey Circle posts to form the 3,4,5 triangles. Carefully position this red triangle such that the "adjacent" and "hypotenuse" crossing vectors touch the sides of Aubrey Circle posts then observe all other sides of the triangle to see the relationships to post positions elsewhere within the site. It will become quickly apparent that the Aubrey and other posts were carefully positioned to relate to 3,4,5 triangulation onto the embankment (star alighting) circle.
Figure 43: A second animated and movable 3,4,5 triangle, this one a mirror image of the first.