TO THE FAR ISLES AT THE VERY ENDS OF THE EARTH.
It
is evident that Viking ships, amongst many others from the ancient Mediterranean,
Continental European seaboard and Britain, sailed successfully to the Antipodean
Isles of New Zealand at the very ends of the Earth in antiquity. If these early
mariners could reach such a remote place, the most distant habitable country in
the world from Europe, then every other part of the globe lay within their reach.

To
the left is seen a belt buckle, retrieved from a Viking burial ship at Sutton
Hoo in England. To New Zealanders and others of the South Pacific Islands, the
face is very recognisable as "Tiki" or "Rongo". He is seen
to be wearing the "high hat", so typically displayed on the statuettes
or totems of the Pacific Islands, ranging from Hawaii to Tahiti to the Cook Islands.
Although the elongated forehead or high hat design aspect is sometimes seen in
New Zealand, "Tiki" or "Rongo" is generally depicted locally
without his hat, as in the old photo to the right. Note how the Maori individual
in the photo emulates the bulging eyes, protruding tongue and facial grimace of
the totem figure and also holds a "mere" club (shaped like the Egyptian
"SA" symbol hieroglyph, meaning "protection"). The origin
of this cultural-religious expression is very ancient and, for both Scandinavia
or the South Pacific totems, goes back to the dwarf god, Bes, of Egypt... who
became Pan of Greece, Puck of Britain and Puge of Scandinavia. Maori oral tradition
states that the arts of carving, facial tattooing and (haka) dance were taught
to them by the earlier inhabitants of New Zealand, who they described as kiri
puwhero (light complexion, reddish skinned) and uru-kehu (light coloured,
golden tinged or reddish hair). For more information on the "world's-apart"
relationship between "Bes" of Egypt and "Tiki"of the South
Pacific or evidence of "Thor" in an ancient New Zealand totem and volcano,
CLICK HERE.
By about 5000
BC and thereafter, the forebears of the European nations abandoned their increasingly
arid homelands in Egypt and its environs and moved to the verdant new territories
of Europe. In doing so, they brought their Weights, Measures and Volumes
standards with them, as well as all of their astronomical and navigational
sciences. These sciences they had encoded (by way of distance, area and angle
numerical codes) into their early-epoch great edifices, like the many pyramids
that they built in Egypt. It must be realised that the Egyptian pyramids of the
Giza Plateau or those at Saqqara are far older than "officially" recognised.
The measurement standards found encoded onto these "Bureau of Standards"
edifices survived for further millennia within the European nations and were,
over time, carried abroad to far-flung locations like New Zealand, by European
explorers and settlers such as the Vikings.
EGYPT,
FORMER HOMELAND OF SEVERAL EUROPEAN NATIONS.
The commonly
known and preserved measurements of ancient Europe, despite their wide variety,
are a part of a single and widely versatile integrated mathematical system, with
traceable root origins and pedigrees extending back to Egypt and its former Caucasoid
ethnicity peoples, who occupied Egypt and surrounding countries for many thousands
of years. Skeletons, mummies, busts, etc., of the forebears to the Nordic Europeans,
are still found there in profusion beneath the desert sands, attesting to their
long occupation of the region.
Let us now look at the mathematical
fingerprints of but one of the many European nations, the Swedish, and
demonstrate how their oldest known Weights, Measures and Volumes standards
have a direct pedigree to the Great Pyramid of Egypt or to its slightly smaller
counterparts, the Khafre Pyramid, which was Egypt's Pyramid of the Moon, and Menkaure
Pyramid.
SAVED BY AN INCH
It's very
inportant to realise that the British Standard inch is not British at all, but
has a very ancient pedigree back to the Eastern Mediterranean and beyond to yet
more ancient Caucasian homelands. The so-called British Standard inch became the
basis of many ancient "cubits" or "foot" measurements, ranging
from Northern India to Egypt or wherever the forebears to the European nations
settled and established long-term civilisations.
THE SWEDISH
MILE.
A Swedish "mil" (Sw. mile) was in
the old days = 6000 "famn" (fathoms) = 18000 "aln" (ells)
= 36000 "fot" (feet) = 10688 meters = 6.64 miles (Hans Högman).
Hans
Hogman speaks of a length equating to 10,688 metres as representing one
of the many increments called "the mile" in use in various parts of
old Scandinavia. The, now, slightly drifted length identified would translate
to 35,066 British Standard feet.
By comparative analysis
to a wide range of other Swedish measurements, which would all have been in direct
ratio or factorable, smaller expressions of the larger increment, it is evident
that the original intended distance of this particular "Mil" or "Mile"
was 35000 standard British feet. Three such "Mils" equated
to 105000 feet or 20 Greek miles of 5250 feet each. Alternatively, three
such "Mils" (105000 feet) equated to 10,000 Hebrew Reeds of
10.5 feet each or 100,000 Greek feet of 12.6-inches each.
Note:
The Great Pyramid was built to be 756 feet in length, which is 72 Hebrew Reeds
or 720 Greek feet. This length also equates to 360 Assyrian cubits of 25.2-inches
each.
Hogman states that the Swedish "Mil"
was divided up into 6000 Famn, which would mean that a Famn was 5.83333
feet or 70-inches. This increment is related to the well known Roman "Pace"
increment of 58.33333-inches (58 & 1/3rd). Therefore, 1.2 Roman
Paces would equate to 1 Swedish Famn. At the same time there would
be 7200 Roman Paces in a Swedish "Mil" or 36000 Roman feet of 11.66666-inches
each. There would be 777.6 Roman feet in the 756 feet length of the
Great Pyramid or 5400 Roman feet in a Greek Mile of 5250 feet.
Note:
There were two readings of the Roman foot, depending on the calculation
requirements. For certain calculations it was read as 11.664-inches, making
a Pace, under that second system, equate to 58.32-inches. This second
reading was used for lunar cycle calculations, as well as some volume measures
The
Roman foot was found to be 11.664 inches by John Greaves, professor of
geometry, who in 1639 went to Rome specifically to ascertain the length of an
ancient Roman foot. Greaves located a monument of Roman architect, Stalius Asper
and measured bas relief instruments used by him in the first century A. D. Greaves
concluded, after careful investigation, that the Roman foot, 'contained 1944
such parts as the English foot contains 2000'. This means a Roman foot of
11.664 inches (11 & 83/125ths).
The Swedish "Aln"
was 1.94444 feet or 23.3333-inches (23 & 1/3rd). This is very consistent
with the report concerning the Rydaholmsalm:
'The
first unit of length to all parts of Sweden was the Rydaholmsalm (the length of
a prototype kept in the church of Rydaholm, Smaland, now lost. It is thought to
have been 0.593 m.'
http://hem.fyristorg.com/ojarnef/fys/se-units-comp.txt
At
exactly .593 m., the Rydaholmsalm would translate to 1.945 feet or 23.34-inches.
We can safely call this a very slightly "drifted" increment that was
known elsewhere as the "Aln", which was related to both the Swedish
Famn and the Roman Pace. The degree of error at the estimated .593
m is so negligible that the 1.944444 feet (23 & 1/3rd inches) proves
to be the intended value of the ancient measurement.
Hogman
further states:
'The "mil" was divided
into 4 "fjärdingsväg" (4 quarters) of 2672 meters or 4500
"aln" (ells).'
From this we can safely assign
an original value of 8750 feet to a "fjärdingsväg"
or 1.66666 (1 & 2/3rds) Greek miles of 5250 feet each.
'1
"steg" = 1/2 "famn" (fathom).'
A
"Steg" was, therefore, 35-inches.
'1
" famn" = 6 "fot" (Sw. feet) = 3 "aln" (Sw. ells).'
From
the above statement by Hogman, we get further verification that the ancient Swedish
"foot" was 11.66666 (11 & 2/3rds) inches and was exactly
the same length as the Roman foot.
It is significant that
one ancient means for easily remembering the equatorial size of the Earth was
to apply the formula:
12 x 12 x 12 x 12 x 1.2 = 24883.2-miles.
If navigating by the Swedish-Roman-Greek method, those miles would be 5250 feet
each (6&7 number family). If navigating by the British method, those miles
would be 5280 feet each (11 number family). The length of the Great Pyramid is
756 British feet or 777.6 Swedish feet. If the Earth is considered, by
the above formula, to be 24883.2-miles in equatorial circumference, then 777.6-miles
would represent 1/32nd segment. Therefore, one of the inbuilt codes of the
Great Pyramid, extractable by use of a Swedish foot of 11.6666-inches (representing
miles), would be to consider that 1 circumnavigation of the Pyramid mnemonically
identified the distance value for 1/8th of the equatorial circumference of the
Earth or 45-degrees of arc.
Hogman states:
'In the
beginning 1 "kabellängd" [cable length] = 100 "famn".'
This
means that the original "kabellängd" was 58.33333 feet
or 60 Roman & Swedish feet. This also equates to 12 Roman Paces.
One
of the concepts of ancient metrology, which survived into mediaeval times, was
that 75 Roman miles represented 1-degree of arc for the world. The Scandinavian
system was, undoubtedly, adopted by the Romans and has its root origins much further
back in remote antiquity. Under this system, the equatorial size of the Earth
was considered to be, for navigational purposes, 25000-Greek miles in circumference
or 131250000 British Standard feet of 12-inches. This distance would also
be 135000000 Swedish-Roman feet of 11.6666 (11 & 2/3rds) inches.
Under
this system, 1-degree of arc (1/360th of the equatorial circumference) was 375000
Swedish-Roman feet. Therefore, according to the oral tradition handed down
from mediaeval times, the Roman mile should have been 5000 Roman feet or 1000
Roman Paces of 58.3333-inches. This equated to 3000 Swedish Alns of 19.4444-inches
each.
Under this system 1-minute of arc (1/60th of a degree) was 6250
Swedish-Roman feet. This equated to 375 Swedish Alns.
Under this
system, 1-second of arc (1/60th of 1-minute of arc) was 62.5 Swedish Aln's.
Hogman
states:
1 "fot" = 2 "kvarter" = 12
"tum" (verktum) = 1/2 "aln"
From this
we see yet further divisions to the Swedish foot and aln. There
was also the "tvärhand", which was 4 "tum".It
would appear that 1/16th part of the Swedish foot was the "fingerbredd".
As
stated, both the Swedish and the Romans appear to have used two separate, but
almost identical, "foot" rules. One "occasional use" calibration
of the foot, set to 11.664-inches (1458/125ths) for lunar cycle tracking, was
marginally shorter than the navigational foot rule of 11.6666-inches. The difference
in the two rules would have been visually difficult to detect.
SO,
HOW DID THE VIKINGS NAVIGATE AT SEA USING THIS MEASUREMENT STANDARD?
When
sailing, one is at the mercy of the wind to a large degree and must tack at angles
to the breeze to make forward progress. The preferred course is not always directly
or easily achievable and tacking, first one way then another at an angle to the
wind, is often the only way to stay on course. It was the ominous responsibility
of the navigators to always be aware of the ship's position and distance from
both point of departure or destination. The navigators had to be constantly aware
of boat speed through the water, as well as heading. Distances covered could be
measured under several systems, such as the "11" family of numbers (leagues,
miles, furlongs, etc.) or other increments of length within a "6&7"
family of special navigational numbers. The Swedish, Romans and Greeks seemed
to prefer the "6&7" family of numbers for "linear distances"
covered or legs completed during a voyage.
The navigators
would maintain a vigilant watch on boat speed and could, from time to time, feed
out a knotted rope over the stern and count the time lapse between knots crossing
the barrier aft. There would be tremendous co-operation between the helmsman and
the navigator, who would work together to maintain the same course heading until
a sought after distance had been travelled. The goal of the ever watchful navigator
would be to complete segments of a voyage according to whole number distances
for each leg in, say, Greek miles at known degree angles around from north. If
full attention, related to boat speed and heading, as well as angle of tack and
distance travelled were maintained, then relatively accurate "positional
plotting" was mathematically achievable. The navigator would have a very
good idea where the boat sat in the vastness of the ocean at all times.
Once
a "straight-line" leg was completed, the navigator would rule a line
on the chart and the end of the scaled line would represent the position where
the boat now sat in the ocean. Each time a long or short leg was completed, this
had to be done and a mathematical means had to exist to determine anew the degree
angle back to the point of departure or onward to the port of destination
If
the Viking navigators wished to achieve a "Mil" of travel (35000
British feet or 36000 Swedish feet) for each leg before changing to a new tack
angle, then the result, in turning this linear distance leg (diameter) into a
circle (using PI @ 22/7 or 3.142857143) would be: 35000 feet X PI = 110000 feet.
So, the navigator could now rule a much scaled down line representing
35000 feet of travel onto the plotting chart, then, using half the length of the
line (radius), draw a circle at the end of the line at the position where the
boat was estimated to be situated in the ocean. The circle created accurately
depicted a circumference of 110000 British feet, in which 1/360th part
(1-degree of arc) was 305.55555 feet (305 & 5/9ths feet) or 55.5555 British
fathoms of 5.5 feet each.
Note: the original British
fathom was 5.5 feet and not 6 feet).
Another metrologist (reseacher
of measurement standards), Gary Anderson, who devoted 10-years to researching
Viking measurements, states:
'Fot*: In doing the research
for this I found that there were actually two measurements for the Fot. One was
very early and ran at exactly 11 inches, the other
was almost 1.03 feet.'
So, with this in mind, the navigator,
using a scaled rule representing "11" inches would know that 333.3333
such increments would represent 1-degree of arc on the plotting chart for the
circumference of a circle with a diameter of 1 Mil (35000 British feet). By this
means, accurate angle fixing back to the point of departure or onward to the destination
could always be known, despite many zigzag course changes during the voyage.
Alternatively,
the legs of the voyage could be accomplished in multiples of "Greek miles"
of 5250 feet, if desired. A circle based upon a diameter of 1 Greek mile would
achieve a circumference of 16500 feet (1 ancient British league...3.125-British
standard miles of 5280 feet each). In this circle, 1-degree of arc would equate
to 550-inches (50 X 11 inches) or 8 & 1/3rd British fathoms per degree of
arc. The so-called Greek mile was fully an increment within the ancient Swedish
navigational system.
From the above, we can see that the Vikings,
along with many other cousin nations, were in full possession of sophisticated
manual methods to do accurate positional plotting at sea. They used one set of
measurement increments, based upon a 6&7 family of numbers, for all of their
linear distance calculations. After the PI formula was used to turn a leg of travel
from a diameter into a circle, the circumference value achieved was easily divisible
by 360-degrees and accurate angle determinations could then be made for positional
plotting. The measurements known to have been used in ancient Scandinavia show
that they knew the equatorial circumference of the Earth and could grid reference
it for accurate navigation and safe traversal using highly factorable numbers.
This
basic rule applies: When travelling by the Swedish-Greek-Roman 6&7 number
family, the circle derived therefrom will be based upon the number "11".
When travelling by the British "11" family of numbers (League @ 16500
feet, Mile @ 5280 feet, Furlong @ 660 feet, Chain @ 66 feet, Rod or Perch @ 16.5
feet, Fathom @ 5.5 feet, Link @ 7.92-inches), the circle derived therefrom will
be perfectly sexagesimal and divisible by 360-degrees. These otherwise strange
numbers, like 5250 feet for a Greek mile or 5280 feet for an English mile, were
specifically created because of PI, so that a linear distance would
convert to a very meaningful circumference that broke down easily into 360-degree
divisions.
ANCIENT SWEDISH VOLUMES FOR DRY GOODS.
Few
things can cause more public discontent than "short measures" at the
market place. When the buying public made a purchase of a "fjärding"
of grain, they expected a full measure for their money. The "fjärding"
had to be the correct cubic inch capacity. Right up until the middle of the 19th
century one could face the death penalty in Sweden for falsifying weights and
measures. It is probably for this reason that there were traditions like "the
baker's dozen", which meant that when one purchased 12 bread rolls, the baker
would include an extra roll to bring the tally up to 13. By such means there could
be no argument that one had been "short changed" or "ripped off"
by the deceitful merchant.
Like all of the other European cousin
nations, the Swedish had a "volume" system with root origins
that extended all the way back to the former homeland of Egypt. Every volume had
to encode scientific information in the numerical value of its cubic capacity.
These special inbuilt numbers, to do with navigation or astronomy, had to be remembered
at all cost, as the concept of civilisation and abundant society depended on them.
If everybody was using the special numbers every day in a length, volume or area
calculation, based upon the selfsame inch, or in weights based upon counts of
healthy wheat grains, then the sciences would never be forgotten. The old adage
applies: "You either use it or lose it".
Hogman
speaks of a Tunna (Barrel):
1 "tunna" = 2
"spann" = 8 "fjärding" = 32 "kappar" = 56 "kannor"
(pitchers) = 146.6 liters levelled measure (struket mått).
Hogman
also says that there was a slightly larger capacity Tunna.
'...or
164.9 liters full (good) measure (fast mått or med råge).'
So,
there was a larger and a smaller Tunna, one at 164.9 litres capacity and
another at 146.6 litres capacity. Let's now convert these ancient volumes
back to cubic inches in an effort to identify the inbuilt, original codes obscured
by metrification.
The larger Tunna, said to have been 164.9
litres would translate to 10062 cubic inches.
The smaller Tunna, said to have
been 146.6 litres would translate to 8945.5 cubic inches.
These
values are very close to highly significant numbers from the ancient parcel of
scientific codes. It is quite obvious that the latter era "Tunna" values
had drifted slightly off the accurate capacity numbers that the ancient forebears
put in place. This can be demonstrated in a very practical sense in consideration
of the smaller divisions or breakdown capacities associated with the Tunna.
It
must be realised that the original architects of these cubic inch or cubic foot
volume systems used highly factorable numbers. A smaller capacity was an exact
division of a larger one. Moreover, the capacity system of one nation would be
in an exact and easily calculable ratio to that of a trading cousin nation. Everything
could be calculated out and transactions done with exactitude by applying simple
ratios or fractions. By looking at the smaller divisions of the Swedish Tunna,
we can easily see what the original volumes were supposed to be, despite small
"drift" that has occurred to the standard within the last 2000 years.
Hogman
states that the capacities of the smaller divisions were:
1
"fjärding" = 18.32 liters (117.9 cubic inches), 1 "kappe"
= 4.58 liters (279.47 cubic inches), 1 "kanna" (pitcher) = 2.617
liters (159.69 cubic inches).
Hogman further states:
"Skäppa"
is a very old measurement that was abandoned in Sweden in 1735. The size of a
"skäppa" could be different in different parts of Sweden. In the
province of Småland a "skäppa" was 1/6 of a "tunna"
(barrel) but in the province of Bohuslän it was only 1/4 of a "tunna"
(36.6 liters) and in the province of Västergötland it was 1/5 of a "tunna".
From
this we can see that the Bohuslän "Skäppa" was
approximately 36.6 litres (2233.3 cubic inches).
From this
abundant accumulation of evidence, we are able to make the very minor adjustments
necessary to restore the intended values put in place by the original architects
of the system. We know full well that they would never have used such utterly
meaningless and arbitrary values as 279.47 cubic inches for a "kappe",
when the highly factorable and full number, 280 cubic inches was available.
Likewise, the value of the "kanna" was not chosen by the Swedish
forbears to be the non-factorable and non-divisible value of 159.69 cubic inches,
but was set at the highly usable value of 160 cubic inches, etc.
So,
let's now restore the original system:
| Swedish
dry volumes (Heavy) | Swedish
wet volumes (Heavy) |
| Large Tunna = 10080
cubic inches. | Fat (Barrel) = 9600 cubic inches. |
| Large
Fjärding = 1260 cubic inches. | Tunna = 7680 cubic
inches. |
| Large Kappe = 315 cubic inches. | Ankare
= 2400 cubic inches.* |
| Large Kanna = 180 cubic
inches. | Fjärding = 1920 cubic inches. |
| Large
Skäppa (Bohuslän) = 2520 cubic inches. | Kannor
= 160 cubic inches. |
| Large Skäppa
(Västergötland) = 2016 cubic inches. | |
| Large
Skäppa (Småland) = 168 cubic inches. | |
| Swedish
dry volumes (Light) | Swedish
wet volumes (Light) |
| Small Tunna = 8960
cubic inches. | Fjärding = 1890 cubic inches. |
| Fjärding
= 1120 cubic inches. | Kanna =157.5 cubic inches. |
| Kappe
= 280 cubic inches. | Stop = 78.75 cubic inches. |
| Kanna
= 160 cubic inches. | Kvarter = 19.6875 cubic inches.
(19 & 11/16ths). |
| Skäppa (Bohuslän)
= 2240 cubic inches. | Jungfru = 4.921875 cubic inches.
(4 & 59/64ths). |
| Skäppa (Västergötland)
= 1792 cubic inches. | |
| Skäppa
(Småland) = 149.3333 cubic inches. | |
Note:
the Heavy Skäppa values are assumed to exist, based upon the Heavy Tunna
value. This is consistent with the way many of the very ancient Mediterranean
systems were structured, offering two differing capacities called "Heavy"
& "Light" or "Single" & "Double" within
a standard. The Skäppa was considered to be a Swedish "Bushel"
and, for the most-part, hovered quite close to the British Bushel, which was,
anciently, 2160 cubic inches. The astronomical coding
placed within the British Bushel related to the duration of the Precession of
the Equinoxes (25920-years) and how the sun spends 2160-years
in each of the 12 houses of the zodiac during the precessional cycle.
*Footnote:
Hogman tells us that the "Ankare" was for volumes of 'Liquor, Wine &
Beer'.
By the description Hans Högman gives of what
we could term as the "light" capacity wet volumes, the values given
make a great deal of sense, despite their visual complexity. The value of 1890
cubic inches was for "navigation", as well as for very accurate
calendar calculation determinations, especially lunar, and the length of the Great
Pyramid is 189 feet X 4 (756 feet). The smaller division value of 19.6875
(19 & 11/16ths) was much used by the Egyptians, Greeks and Romans and
their Beqa weight Standard for gold was set at 196.875
grains. Further verification and comparitive
analysis will be necessary to fully determine if that family of navigational and
lunar numbers was being used within the Swedish wet volumes standard, but it is
certainly looking very encouraging so far.
Note:
the "Stop" volume for the Wet "Light" series appears
to be 78.75 cubic inches. The Viking longship found at Oseberg, Norway
(circa 1904) had a length of 78.75 Swedish
feet of 11.666666-inches (11 & 2/3rds). Half the base length of the Great
Pyramid (378 feet) is in a ratio of .7875 to 1
to the height (based upon where lines running up the faces would converge at a
single point above the flat floor altar at the top of the Pyramid & coded
to be at 480 feet of vertical height). The
width of the Oseberg longship was 17.5 Swedish feet, for a length to width ratio
of 4.5 to 1.
WHAT IS THE
UNDERLYING SCIENCE ENCODED INTO THE OLD SWEDISH DRY VOLUMES?
To
understand the significance of the numbers encoded into these cubic capacities,
one must return to analysing the dimensions of the Great Pyramid of Egypt, situated
in the former homeland of Nordic Europeans, but long ago abandoned to the encroachment
of the desert sands.
The Great Pyramid was designed to be 756
feet per side length or 3024 feet for one circumnavigation. Under what, much later,
became the Swedish-Greek-Roman method of world-traversing navigation, two circuits
of the Great Pyramid were 6048 feet, which represented 1-minute of arc on the
Earth's circumference. The full equatorial circumference under this method was
24883.2 "Greek" miles of 5250 feet each or 130636800 British standard
feet. This meant that 1-degree of arc (1/360th of the Earth's circumference) was
362880 feet (note that one full circuit of the Great Pyramid, which means 756
feet x 4 or 3024 feet = 36288 inches). As stated, 1-minute of arc (1/60th of a
degree) was 6048 feet and 1-second of arc (1/60th of 1-minute) was 100.8
feet. There would be 7.5 occurrences of 100.8 feet in
one side length of the Great Pyramid.
Note:
The Sarsen Circle at Stonehenge (made of upright Sarsen stones capped with lintels)
was made slightly eliptical to achieve two sets of crossing codes. In one cross
measurement the Sarsen Circle is 100.8 feet, or 1-second of arc diameter for the
equatorial circumference of the world.
The value of
10080 cubic inches in the Swedish Heavy
Tunna is a very important navigational value, alluding to the number used
to describe 1-second of equatorial arc. It was placed into the standard for mnemonic
recall of the size of the Earth. In each of the lesser divisions of the Large
Tunna there are recurring progressions of numbers that can be exploited for world
navigation.
There is insufficient room in this article to demonstrate
all that these volume codes could do or mean and researchers are encouraged to
refer to Weights, Measures and Volumes of the Ancient
Mediterranean, within this website.
To see that fuller article CLICK
HERE.
A small glimpse of how far one could go
in extracting meaningful codes is seen in the conversion of "1-second
of arc" (100.8 British standard feet) into ancient Swedish units based
upon their navigational foot of 11.6666-inches. Therefore, 100.8 feet x
12 = 1209.6 inches ÷ 11.6666 = 103.68.
Consider this:
The ancient value for the equatorial size of the Earth was 24883.2-miles. There
are 24 hours in a day so the rate of speed at which the Earth spins is 24883.2
÷ 24 = 1036.8 Miles per hour.
Consider also: One half
of 103.68 is 51.84. The slope angle of the Great Pyramid's 4 faces is 51.84-degrees.
The azimuth angle from the altar of the huge Octagon earthworks complex of
Newark, Ohio, dissecting the entire site in half and extending through the avenue
out the end gate of the Octagon, is 51.84-degrees. The Precession of the
Equinoxes endures for 25920-years, which is 51.84 x 500. When one travels
1 British league of 16500 feet (3.125-miles), it converts to a sexagesimal navigational
circle of 51840 feet (divisible by 360-degrees).
Consider also:
The "Stirling Jug" of Scotland, dating to 1457 and possibly much
earlier, had a capacity very close to 103.68 cubic inches, which was the
same as the ancient Hebrew liquid volume called the Jerusalem Cab (predating
the Babylonian conquest), etc., etc.
The smaller Tunna is 1.125
to 1 less in size to the large Tunna, so it's a perfectly ratioed down expression
of the bigger one.
BUILDING A "TUNNA" ROUND BARREL
OF PERFECT INTERNAL CAPACITY.
As stated earlier, up until
the middle of the 19th century, one could face the death penalty in Sweden for
falsifying weights and measures or conspiring to deliberately defraud the buying
public. This meant that merchants in the market place had to have perfect capacity
vessels, such that anyone purchasing a "Tunna" of grain received
exactly what they had paid for. Market place inspectors periodically checked the
accuracy of the merchant's measuring tubs. So, how did the ancient Swedes produce
round barrels or tubs that they knew, with certainty, were of perfect, internal
cubic inch capacity?
The answer to that question lies in the
fact that the ancient people of Scandinavia had yet another measurement rule of
1.030 British Standard feet, which functioned specifically for creating
all of the various volume vessels or tubs. Gary Anderson, who researched Viking
measurements for ten years, concluded that there was a very old "Fot"
(foot) that would equate very closely to .314 metres. This would translate
to 1.03018 feet. http://www.vikingage.com/vac/measuring1.html
The
manner in which the ancient scientists configured these highly specialised rules
for constructing round volume vessels, was to base them
on the PHI ratio of 1.6180339 to 1. The same ratio exists between the
area covered by the base of the Great Pyramid in comparison to the area of its
4 side faces, including a symbolic capstone on top.
If
one uses simple trigonometry to work out the side length of the full pyramid,
including the theoretical, non-existent capstone, the length to the centre apex
would be (Adj. ÷ 51.84 Cos.) = 611.7894615 feet.
Alternatively,
if one used a PHI method of Adj. (378 feet) X PHI (1.6180339) = 611.6168142
feet.
It will be observed that the calculated PHI length
is only about 2 inches less than the length achieved by straight trigonometry.
The ancient astronomer/ mathematicians were coding a PHI related angle for the
Great Pyramid simultaneously to the standard angle of 51.84-degrees. The
whole edifice was designed to clearly code PHI relationships. For example:
Let's consider the Great Pyramid on the basis of PHI and the ratio relationship
(in pyramid acres) between the 4 faces, compared to the ground area that the
Great Pyramid covers.
The surface area of each face of the theoretical
full pyramid, complete with a (symbolic) pointed capstone, = 611.6168142 feet
of side length X 378 feet (1/2 the base length) = 231191.11558 square feet.
Because there are 4 faces, their combined square footage
amounts to 924764.6231 square feet. This translates to 32.10988275 pyramid
acres of 28800 square feet each.
The base area measured 756 feet X 756
feet or 571536 square feet, which equated to 19.845 pyramid acres of
28800 sq. ft each. A perfect PHI relationship exists between this (symbolic
capstone included) total side acreage and that of the base area that the Great
Pyramid covers: 32.10988275 ÷ 19.845 = 1.6180339
(PHI).
Because the
Great Pyramid was a static "Bureau of Standards" for the Caucasoid family
of scattered nations and civilisations, it was absolutely
essential that it strongly encode the PHI ratio, as this was central
to fabricating very accurate, circular"volume vessels"
or tubs with ease. Evidence shows that all of the most ancient volume
vessels were made by this simple method. The use of the PHI formula persisted
through the epoch of the Druids until the dawn of the "Dark Ages", spawned
by the coming of Roman Christianity and its brutal introduction of backwards,
dogmatic religion. Prior to that time, all volume vessels had to contain profound
codes in (1) the square inch area of the base, (2) internal side
height and (3) cubic inch volume, all of which related to astronomical
cycles or world navigation.
NOW, BACK TO HOW THE
SWEDISH SCIENTISTS WERE USING THE PHI RATIO.
To make perfect
capacity, round volume vessels for the Swedish Tunna of 10080 cubic inches
the formula was:
10-inches ÷ 1.6180339 (PHI) = 6.18034-inches
(this increment became the standard length for making all of the circular
market place volume tubs, of widely varying capacity, for all of the cousin European
nations.
The
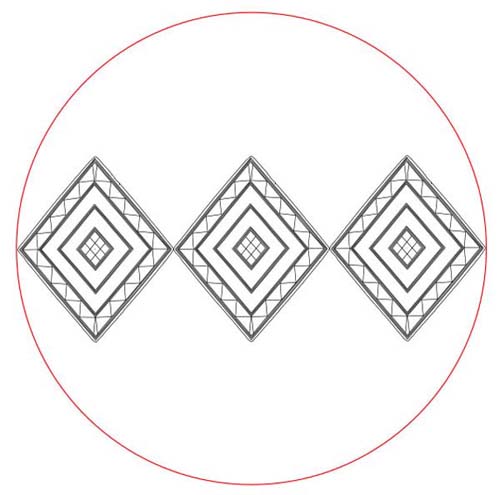
width of the Bush Barrow Lozenge of Southern England was very close to 6.18034-inches
(the lozenge has suffered some edge damage, slightly obscuring the original codes)
and two such widths equated very visually close to 12.36068-inches or 1.0300566
feet, seemingly the same as a Swedish long "Fot".
A primary purpose of the Bush Barrow Lozenge appears to have been for "market-place"
inspectors to check the base width of "Bushel" barrels and tubs used
by ancient merchants of the Neolithic Age. The very slightly "drifted"
dimensions, for building a Bushel tub, are described in the old "English
Winchester Standard". The base floor of the British Bushel was 270 square
inches, with walls rising above the base floor a total of 8-inches, for a cubic
capacity of 2160 cubic inches.
The increment of 6.18034
X 2 = 12.36068-inches. This value equates to 1.03005666 feet and
is the measurement identified by researcher Gary Anderson as the largest
"Fot" utilised by the Vikings.
In the following
I will show numbers set at decimal point refinement and tolerances beyond what
was visually or manually achievable by humans, but do so only to demonstrate how
perfect the ancient mathematical method was.
To make the
Tunna tub base, take a large thin slab of flat smooth timber or tightly edge-splice
several planks together to form a single piece of sufficient size. Next take the
1.0300566 foot rule and mark double that length (2.0601132 feet)
onto the wooden base. Now take a compass and create a circle of 2.0601132 feet
diameter. Because you have used a rule derived directly from the PHI formula,
your base is exactly 480 square inches of surface area. Your formula for
determining the square inch area is PI x the radius squared, memorised
by every schoolchild in the formative years of their education. So, the diameter
of 2.0601132 feet ÷ 2 = 1.0300566 feet = 12.3606792-inches.
This value "squared" = 152.7863903 x PI (3.14159) = 480
square inches of base.
The
480 number is a much used coded value of antiquity
and all aspects of your tub must contain recognisable codes in the base surface
area, internal side height and cubic capacity to be contained. Because you need
to achieve a cubic capacity of 10800 cubic inches for this Swedish Tunna
vessel, the internal height of the tub, from the top surface of the base to the
brim of the side wall is 21-inches. This value (21-inches...sometimes called
a Celtic Royal Cubit) is found in the base length of the Great Pyramid, which
is 432 X 21-inches in length per side or 1728 X 21-inches for all four sides.
Note: A cubic foot (12 x 12 x 12) is 1728 cubic inches.
It's
as easy as that to make all of the old Swedish volume vessels listed and have
them achieve a perfect capacity. You have the option to use 1, 2, 3
or more of the 6.18034-inch PHI-derived increments in the base. A tub can
be more squat than tall or vis-versa. A perfect capacity is always easy to create
by this simple ancient method, which was used in the production of, seemingly,
all the tub-type standard volume vessels of the Caucasian (European) civilisations
in antiquity.
NAVIGATIONAL
AIDS
The Scandinavian mariners
are known to have used the Sun Shadow board of 32 calibrations for navigation
and are theorised to have used a Sun Crystal for determining the sun's rise and
set positions on cloudy days. Other than that not much has survived to tell us
how they did "dead reakoning" or "positional plotting"
to stay abreast of their location in the open sea. A very good clue, however,
to the kinds of devices they would have used, is found in the Bush Barrow Lozenge
or Clandon Barrow Lozenge artefacts of Southern England.

The
Bush Barrow Lozenge and associated artefacts located in Southern England, very
close to Stonehenge. The intricate pattern incising is far more than decorative
and with a set of callipers and a precise rule, a wide variety of codes can be
extracted from the main lozenge.
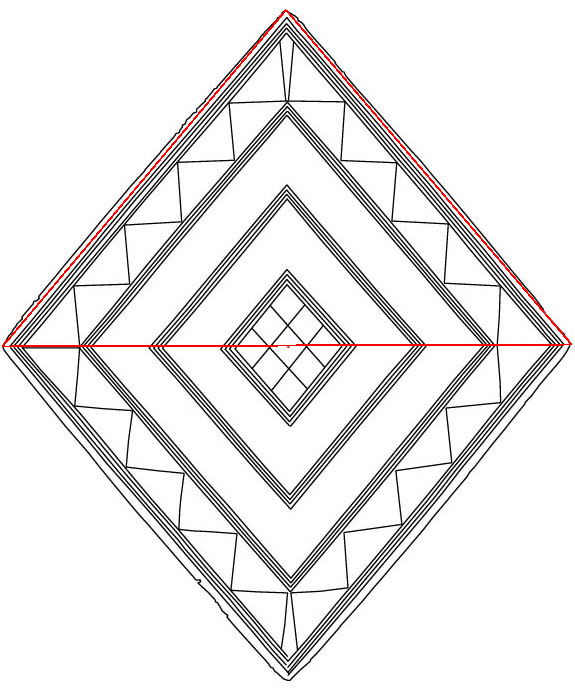
There
were once, undoubtedly, a wide variety of "Lozenge" memory devices,
used for a range of functions including navigation at sea. For the Viking navigator,
remembering the coded dimensions and geometry of the Great Pyramid and that of
the Khafre Pyramid, would have been sufficient. If those encoded principles were
committed to memory and the lozenge mnemonic devices were fabricated as precisely
"scaled" rules in their side lengths or other internal reducing diamond
patterns, then accurate positional plotting at sea was very achievable to the
experienced navigator.
Consider the following:
- The
ancient coding for the equatorial size of the Earth, as found on the Great Pyramid
is 12x12x12x12x1.2 = 24883.2 Greek miles of
5250 feet each. The height of the Great Pyramid is coded to represent 480
feet of vertical height at the point where lines coming up diagonally
from each face side intersect in the air above the flat floor altar. The sum of
24883.2 ÷ 480 = 51.84,
which just happens to be the slope angle of each face of the Great
Pyramid (51.84-degrees).
- The
more difficult trigonometric method for finding the hypotenuse length of the Great
Pyramid sides (378 feet Adjacent ÷ 51.84 COS = 611.789 feet
is very easily accomplished by using the PHI formula. Therefore: 378 feet x PHI
(1.6180339) = 611.6168 feet (a difference of about two inches in the hypotenuse
lengths). What this tells us is that the angle 51.84-degrees, based upon a navigational
triangle, the adjacent of which is scaled to represent 1/16th of 1-minute of equatorial
arc, is created to very good relative accuracy by a simple manipulation of PHI
(1.6180339). One could, thus, state that a 90-degree triangle with a hypotenuse
angle of 51.84-degrees (as incorporated into
the Great Pyramid geometry) has a hypotenuse length that is a PHI
increase on the adjacent length. Therefore, the angle of 51.84-degrees,
under such geometric design circumstances, could be called a PHI
generated angle.
- The
sum of 51.84- miles would be 1/480th of the equatorial circumference under the
Great Pyramid's geodetic system or .75 of 1-degree of arc.
- We
therefore can use a navigational triangle where the "Opposite"
is considered to be 480 feet, where the "Adjacent"
is in a ratio of .7875 to 1 to the "Opposite"
and where the "Opposite" is in a ratio of .7854
(1/4th PI @ 3.1416) to 1 to the "Hypotenuse".
THE
VIKINGS AND THEIR FOREBEARS KNEW THE EXACT SIZE OF THE EARTH.
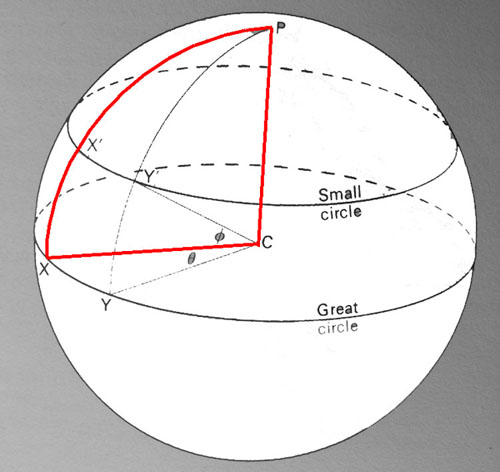
The
Red segment accentuated in this image from a book
on "Positional Astronomy" demonstrates exactly what the Great Pyramid
triangle was supposed to encode. The Great Pyramid
triangle taught spherical geometric and trigonometric principles for safe navigation,
but also contained mathematically extractable information related to the EXACT
equatorial circumference of the Earth. The following is what early pre-Christian
European navigators had to commit to memory and what they handed on generation
after generation to their progeny, until the Roman Christian Church finally destroyed
their old scientific knowledge:
- In the coded navigational triangle
of the Great Pyramid the "Adjacent" (half the base length) was 378 feet
and this distance was 1/16th of 1-minute of arc under the Swedish-Greek-Roman
method of reading the Earth's equatorial circumference.
- The Great
Pyramid triangle, however, had to demonstrate to the student of navigation the
ratio that existed between the earth's radius and its
outer curved face. This was, quite obviously, taught (in view of the
Great Pyramid's triangular design configuration, coupled with its scaled geodetic
attributes) by using a quarter segment of the Earth's circumference, as shown
in the red segment in the picture. The horizontal line X to C represents
the radius of the Earth, from the equator to the centre of the Earth. On the Great
Pyramid triangle this world dimensional radius was represented by the vertical
height (Opposite), coded to be 480 feet. If we consider the Earth's diameter to
be 7920-miles, then its radius is 3960-miles. The reduced sum of 480-miles would,
therefore be in a scale of 1 to 8.25 against the true radius.
- The
480 feet Opposite, however, had to be in a ratio of .7854
to 1 to the distance measurement of the face (Hypotenuse) of the Great
Pyramid triangle. The PI ratio for converting a circle's diameter to a circumference
is 1 to 3.1416, thus the
.7854 to 1 value is 1/4th of PI. In the above picture the curve red
line represents 1/4th part of the sphere or 1/4th PI.
- To achieve a distance on the Great Pyramid's Hypotenuse or face
that demonstrated a ratio to the Earth's radius, compared to its curved outer
or spherical surface, either a PHI (1.6180339 to 1) increase on the Adjacent was
used or else the Opposite (480 feet) ÷
1/4th PI (.7854) was used. So, 378 feet X 1.6180339 = 611.6168142
feet (the length of the Great Pyramid's faces to where all diagonally
upward lines resolve to a common apex point). If this Hypotenuse length is multiplied
by .7854 (1/4th PI @ 3.1416) then the value
achieved for the Opposite or vertical height is 480.3638459
feet or very close to 480 & 4/11th feet. By this means a wonderful
tutorial is available to teach the ratio difference between the
radius of a sphere (like the Earth) and quarter
of it's circumference. It should be noted that
trigonometry dictates that the apex height of the Great Pyramid would have sat
between 480 and 481 feet of vertical height, in consideration of a half base length
of 378 feet and a slope angle of 51.84-degrees. There was, of course, never a
capstone on the pyramid only an flat floor altar on top, but the geometric principles
of a "full" pyramid still applied.
- The "Official"
equatorial diameter of the Earth is 7926-miles
of 5280 feet each. The radius of the Earth is, therefore, 3963-miles and its official
equatorial circumference is 24,900.26337-miles.
- If
the above 480 & 4/11th feet were called (coded as) miles, then that would
be in a ratio of 1 to 16.5 on the Earth's diameter or 1: 8.25 to
its radius. Therefore: 480.36363636-miles X 16.5 = 7926
miles for a precise reading of the Earth's equatorial circumference
of 24900-miles.
- For navigational convenience, this value was anciently
set at the highly factorable number of 24883.2-miles
(12x12x12x12x1.2), which, depending on navigational method preference,
could be miles of 5280 feet ("11" family) or 5250 feet (6&7 family).
In all, there were several navigational methods, exploitable within different
number families and the Great Pyramid geodetic or navigational geometry was adaptable
and applicable to them all.
- In this study, we have seen how the
PHI formula was used by ancient Caucasoid civilisations in a very dynamic way
and practical sense for creating highly accurate volume vessels for the marketplace
or tutorials in spherical geometry.
- The exactness of the Great
Pyramid equatorial coding suggests a former age of very advanced technology that
was lost because of a cataclysmic event, in the aftermath of which only some very
specialised knowledge survived. The parcel of numbers describing the duration
of cycles and the equatorial dimensions of the Earth was used to re-establish
and preserve "civilisation".
Other
Great Pyramid attributes that would be committed to memory include:
- The
378 feet increment x 12 = 4536-inches. It just so happens that the flat floor
altar atop the Great Pyramid (which has always been there throughout recorded
history) sits at a height of 453.6 feet. The
equatorial size of the Earth, according to the main Great Pyramid coding is 24883.2
Greek miles or 130636800 feet. This divided by 453.6
= 288000.
- Late
era Egyptian Priests told Herodotus that each face of the Great Pyramid represented
8-Pyramid acres. Given the literal dimensions of the Great Pyramid with its flat
floor altar on top, each face equals 400 feet (756 feet of base length with an
altar floor on top that is 44 feet long) X 576 (the length up the face to where
the altar floor begins) = 230400 square feet. This ÷ 8 = 28800
square feet. Note: the Aubrey Circle at Stonehenge has
a diameter of 288 feet and
the Hypotenuse length up the Menkaure Pyramid was intended to be 288-feet.
Note:
Menkaure Pyramid was abandoned before it was completed... probably about 5000
BC... the Pyramids of Giza are far older
than we're led to believe and there's no real evidence to suggest that they were
built during the Dynastic period. Menkaure Pyramid (misnamed like the rest) was
intended to have a slope angle of 51.84-degrees,
just like the Great Pyramid.
- The
literal sum total of "pyramid acres" in the 4 faces and area that the
Great Pyramid occupies = 756 x 756 of base area = 571536 square feet + 921600
of side area =1493136 square feet. This divided by 28800 (pyramid acre value)
= 51.845 pyramid acres all up...coding 51.84
yet again.
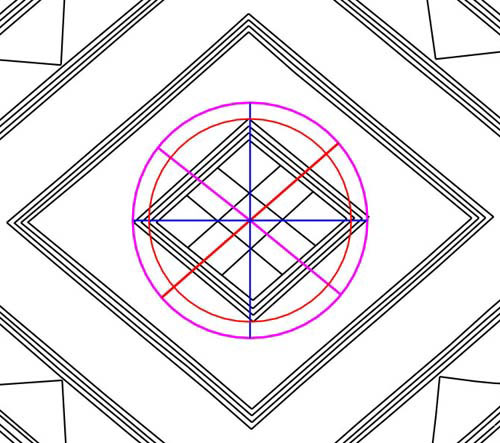
The
Bush Barrow Lozenge centre section, based upon an accurately scaled drawing of
the lozenge done within the exacting confines of AutoCAD. Scaling was completed
by reference to dimensions supplied by Mr. Paul Robinson, Curator of the Devizes
Museum, Wiltshire, England.
- The red line running diagonally
up to the right is on an angle of 51.84-degrees...the
same as the inscribed line on the Clandon Lozenge's centre arm of the St. Andrew's
Cross.
- The magenta line running diagonally up to the left is
on an angle of 311.04-degrees...the
same as the inscribed line on the Clandon lozenge's centre arm of the St. Andrew's
Cross. Under the 24883.2-mile equatorial circumference,
the sum of 3110.4-miles would be 1/8th
of the equatorial circumference or 45-degrees of arc.
- Several
mnemonic codes interplay herein...311.04-degrees minus 51.84-degrees = 259.2-degrees.
The Heel stone outer face at Stonehenge sits 259.2 feet
from site centre at an angle of 51.84-degrees to its south facing side.
There are 25920-years in the Precession of
the Equinoxes. The sum of 311.04-degrees is
360-degrees minus 48.96-degrees. If the value of 48.96-degrees is added to 51.84-degrees,
then the total is 100.8-degrees. The value
of 100.8 feet was 1 second of Earth equatorial
arc under the Great Pyramid "6&7" geodetic assignment, which sized
the Earth to 24883.2-miles of 5250 feet. At
Stonehenge's Sarsen Circle inner rim one of the cross measurements between lintels
was 100.8 feet, coding 1-second of arc.
The
foregoing represents just some of the coding that the Scandinavian navigator (or
any late era Druidic Priest teaching navigation, for that matter) would have committed
to memory for the fluid reading of navigational devices. He had the option of
using a range of cubits or feet measures, including Hebrew Reeds of 10.5 feet,
Assyrian cubits of 25.2-inches, Celtic or Hebrew Royal Cubits of 21-inches, Celtic
common cubits of 18-inches, older Hebrew and Babylonian feet of 17.5-inches or
16.8-inches, Greek feet of 12.6-inches, Swedish-Roman feet of 11.6666-inches,
a measurement identified by Egyptian Priests to Herodotus of 11.34-inches (lunar...3
sides of the Great Pyramid = 2268 feet or 1134 feet x 2), etc., all of which would
fit the literal dimensions of the Great Pyramid. The Egyptian Royal Cubit (one
of 3 types), which is simply a memory device for remembering the equatorial circumference
of the Earth, is 1/440th of the Great Pyramid's length or 20.61818182-inches
(20 & 34/55ths).
Without trying
to confuse the issue, there was another geodetic system built into the Great Pyramid,
which meant extending it's length by 3-inches (756.25 feet per side) by this means
the equatorial circumference could be read in miles of 5280 feet (under an "11"
family of numbers...League, 16500 feet, Mile , 5280 feet, Furlong or Furrowlong,
660 feet, Chain, 66 feet, Rod or Perch, 16.5 feet, Fathom, 5.5 feet, Link, 7.92-inches).
This second method was preserved in Britain and Germany, but the existence of
an "11"-inch rule amongst the Viking measurements attests to the fact
that this navigational system was also used, at times, in Scandinavia.
This
researcher apologises for the complexity of the presentation, but cautions any
wannabe "Druids": This is what a Druid learnt, taught, maintained
incorruptible, held sacred and passed to the ensuing generation. Getting yourself
a nobbled staff and dressing up like a Druid, then watching the Solstice sunrise
at Stonehenge while doing the "Hey derry derry down" two-step dance
doesn't make a Druid... You have to serve the hard-slog
apprenticeship and learn the cyclic and navigational maths!... unless you only
aspire to be a "bard" or "inferior rhymer"... sorry
to be the bearer of ill tidings.
THE OTHER
NAVIGATIONAL TRIANGLE
Along with the main
navigational triangle incorporating a scaled Adjacent that was .7875 the
value of the Opposite and in a PHI relationship between the Adjacent and
Hypotenuse, etc., there was yet another very important one for following the cycle
of the moon.
Obviously, the moon's position
every night is a very good indicator of ship's position, provided the navigator
knows the cycle of the Moon on a daily basis during the lunar year or its larger
duration cycle over 18.613 solar years (anciently set at 6804-days). All of the
scientific information necessary is found on the Khafre Pyramid, Egypt's Pyramid
of the Moon.
The way to find the exact intended
dimensions of the Khafre Pyramid is to realise that it's 15/16ths the base
length of the Great Pyramid. Therefore: 756 ÷ 16 = 47.25 feet x
15 = 708.75 feet. If one dissects the Pyramid
in half from the centre base to the apex, then a 3,4,5
triangle is the result. Half the base length is therefore 354.375
feet and it just so happens that there are 354.375-days
in a lunar year. The dimensions are Adjacent, 354.375 feet (3 x 118.125),
Opposite, 472.5 feet (118.125 x 4) and Hypotenuse, 590.625 feet. All of these
numbers are dynamic lunar values. The inch count around the pyramid is 708.75
x 4 x 12 = 34020-inches (1/2 of 68040 inches). Note there are 6804-days in the
ancient calibration describing the lunar nutation cycle. Also the Adjacent value
of 354.375 (354 & 3/8ths days) ÷ 12 = 29.53125-days (29
& 17/32nds days or 708 & 3/4ths hours). The lunar month is
29.53125-days to a precision of less than
a minute.
It can be readily seen that merely
by memorising the dimensions of these two edifices and then working from precisely
scaled rules, that all or most of the essential navigational mathematics are known.
Moreover, having scaled memory devices like the Bush Barrow Lozenge on hand would
keep the special navigational knowledge at the forefront of memory. Added to that,
the boat itself would be coded according to length and breadth with navigational
measurements, so that a forgotten principle could be recalled by measurements
on board. This would include the volumes contained within the food storage tubs
and vessels, the dimensions of sailor's sea chests that they sat upon when rowing,
the length of oars, the height of the dragon head prow, etc., etc. Rest assured
that no opportunity to build codes into internal positions of the boat would be
missed.
Added to the above, if a boat was
swamped and wrecked, but the navigator and others survived, sufficient to build
a raft or patched up boat on which to limp home, all of the navigational aids
could be restored if the navigator retained a rule or even a belt buckle that
was a true inch wide. The fact of the matter is that the ancient navigational
methods are so sophisticated that, with the aid of an abacus, an adept, well trained,
ever alert and clever navigator could work out Longitude with relatively good
accuracy and Latitude with little else but a shadow pole.
Although
it has been stated by several authors that nothing has survived to indicate Viking
navigational knowledge and methods, a huge amount has, in fact, survived. The
researchers, unfortunately, have been looking in the wrong places. They should
have delved deeply into the most ancient "Weights, Measures & Volumes"
used and preserved by the Scandinavians to find the navigational mathematics.
Swedish,
Danish and Norwegian researchers are encouraged to experiment with the numbers
and simple mathematical methods identified herein. After all, this is your
long-term heritage, based upon your own ancient measurements. Only a very
few of your oldest standards have been touched upon here, but rest assured that
ALL weights, measures and volumes, originally configured for use in each
of the ancient Provinces, would have been from the same wellspring of coded numbers.
As time permits,
many more of the ancient Swedish standards can be identified, then categorised
as to function and number family. The same processes identified herein will
apply to all of the ancient German Weights, Measures and Volumes, as well
as within the oldest standards used amidst any long-established European nations.

A
Celtic Torque, taken from the grave of the Princess of Vix, (circa 5-600 BC).
It weighs 480 grams, which converts fluidly to 16.875 ounces
(16 & 7/8ths). Its carefully fabricated and coded weight is, therefore,
in direct ratio to both the Greek Commercial Talent or Tridrachm (Beqa)
gold standard Talent and it represents 1/80th
of the Talent weight in both standards. The Torque depicts the rising and setting
orb of either the Sun or Moon and shows a "Greek Pegasus" flying horse
ascending upwards on the orb to the East (right) and downwards on the orb to the
West (left). In terms of the grain weights inherent within the artefact or Greek
Commercial & Tridrachm standards, the numbers produced are lunar and 16.875-days
(504-hours) would be 1/21st-part of the lunar year
of 354.375-days duration.
We
will soon analyse the ancient Swedish "Weights" system, based upon "grains".
A cursory assessment shows it to be using the same mathematical progression as
the Hebrew "Desert Heavy Weight" standard, where the Talent,
Mina and Shekel are in direct proportion to the ancient Swedish "Skeppspund".
The internal coding of these related (ancient Hebrew & Swedish) systems of
weights refers directly and dynamically to the lunar cycle and navigation.
Remember,
no pre-Christian weights, measures and volumes standards used by the European
nations were arbitrary and meaningless and all were in perfect ratio, either
within the provinces of the same nation or to the standards of other cousin nations.
The perfect ratios that existed between provincial or national standards allowed
everyone to trade in the same market places around the Mediterranean or Atlantic
and easily convert quantities mathematically. All original standards, put in place
then maintained by overseer scientist-astronomers like the Druids or their forebears,
always contained profound scientific information, very essential to continued
abundant living and optimised society. That scientific information came from a
solitary parcel of highly specialised numbers, handed down from remotest antiquity
and it is still found in the geometry of standing stone circles or via the dimensions
and angles found upon the most ancient edifices of the Mediterranean and Europe.
The
sophisticated astronomical and navigational sciences embraced by your Swedish-Norwegian-Danish
forebears allowed them to sail, at will, to any place on the globe where they
chose to go...even unto the very ends of the Earth.
Martin
Doutré, October 2006. ©
To
be continued.

