Waitapu navigation.

SPECIFIC "OLD WORLD" NAVIGATIONAL DISTANCES AND ANGLES MARKED INTO THE WAITAPU REGIONAL TERRAIN.

The Waitapu Valley region, undoubtedly, functioned as a "School of Learning" where apprentices of the navigational, astronomical and surveying arts could hone their skills by practice and repetition. There was a huge amount to learn and retain in memory.

Particular lengths between overland markers were set out to demonstrate principles of navigation, skills that needed to be acquired before venturing out on intercontinental voyages. The initiate needed to know the size of the Earth under 3 marginally variable systems (working to the numbers 6, 7 &11) and how to grid reference the globe for safe traversal.

Students needed to learn how to use the navigational systems to calculate bearing and distance traveled, despite many course changes of a sail driven ship upon the open sea. Apprentice navigators would have learned to read shadow poles to determine latitude and zenith stars that sat, seasonally, over particular countries at midnight.

Initiates would have been taught about the cycles of the sun and moon, especially the 18.613-year lunar cycle, as the moon was the primary determinant of the weather one would encounter in any clime. The calendar system that was utilised by their ancient society incorporated the cycles of both the sun and moon (lunisolar) simultaneously and was very accurate.

COMPARISONS TO THE SCHOOLS OF LEARNING OF NORTHERN HEMISPHERE COUSINS.

In the ancient societies of the Druids and pre-Druids of Britain and France there was an ongoing conflict between the choice of "memory" to retain knowledge or "writing" it down to ensure its preservation. Druidic Priests preferred to memorise, as the surest way of passing knowledge from one generation to another. Their concern was that writing would make them somewhat lazy and threaten the "diligence of the student".

Although the early Britons continue to be erroneously represented as savage "barbarians" by classicist historians, nothing could be further from the truth. Isabel Hill Elder writes, 'The education system adopted by the Druids is traced to about 1800 BC when Hu Gardarn Hysicion (Isaacson), or Hu the Mighty, led the first colony of Cymri into Britain from Defrobane, where Constantinople now stands'. Further commenting on Hu Gardarn Hysicion, Isabel Hill Elder writes that he, 'is commemorated in Welsh archaeology as having made poetry the vehicle of memory'. Elsewhere she writes, he 'is said to have mnemonically systematized the wisdom of the ancients...'. She goes on to say, 'The published compositions of the Druids and Bards form but a very small portion of the extant remains of their works. The Myvyrian MSS. alone, now in the British Museum, amount to 47 volumes of poetry, in 1600 pages, besides about 2000 epigrammatic stanzas. Also in the same collection are 53 volumes of prose, in about 15,300 pages, containing many curious documents on various subjects...' (see Celt, Druid and Culdee, pages 54 & 55).

Julius Caesar, who was a very thorough historian, writes the following regarding the late era Druids of his time (circa 55 BC) and the practices within their many universities in Britain, where students from Gaul went for training:

'They hold aloof from war and do not pay war taxes; they are excused from military service and exempt from all liabilities. Tempted by these great advantages, many young men assemble of their own motion to receive their training, many are sent by parents and relatives. Report says that in the schools of the Druids they learn by heart a great number of verses, and therefore some persons remain twenty years under training'.

'They do not think it proper to commit these utterances to writing, although in all other matters and in their public and private accounts they make use of Greek characters. I believe that they have adopted the practice for two reasons- that they do not wish the rule to become common property, nor those who learn the rule to rely on writing and so neglect the cultivation of memory; and, in fact, it does usually happen that the assistance of writing tends to relax the diligence of the student and the action of memory...They also lecture on the stars in their motion, the magnitude of the Earth and its divisions, on natural history, on the power and government of God; and instruct the youth in these subjects' (see De Ballo Gallico, VII, 15, 16.).

Isabel Hill Elder further writes, 'The students at these colleges numbered at times sixty thousand of the youth and young nobility of Britain and Gaul. Caesar comments on the fact that the Gauls sent their youth to Britain to be educated...It required twenty years to master the complete circle of Druidic knowledge. Natural philosophy, astronomy, mathematics, geometry, medicine, jurisprudence, poetry and oratory were all proposed and taught-natural philosophy and astronomy with severe exactitude' (Elder refers to Strabo I IV, page 197. Caesars Comm. Lib V. Sueotonius, V Calegula. E. Campion, Accounts of Ireland, pg. 18.).

THE ANCIENT NEW ZEALAND SCHOOLS OF LEARNING.

It will come as a surprise to many that ancient New Zealand once had many advanced Schools of learning, with some remnant knowledge survivals still being passed down through the Maori Wharewaananga.

We know from oral traditions that there was a period of time when newly arrived Polynesian Maori integrated with the earlier Tangata Whenua (the many groups named by Maori under a major heading of Patu-pai-arehe, along with several other regional names). From these early people Maori learned the art of Moko (tattooing) and acquired the many symbols still in their possession, like the double spiral. Although there's little evidence to suggest that the advanced mathematical concepts were passed to Maori, some astronomical knowledge, use of lunar calendar systems for fishing, net making and general crafts were shared. If any of the developed mathematical sciences were handed on, then they appear to have been long-since forgotten, as these sciences are, to my knowledge, absent and not taught in the surviving Wharewaananga colleges. Thankfully, the mathematical knowledge is still encoded into the New Zealand countryside and can be retrieved by surveying the positions of ancient, purpose placed markers.

Let's now look at the repetition of particular Waitapu Valley region lengths (and to some degree angles) in batches and discuss their code bearing attributes:

THE TRUE EQUATORIAL CIRCUMFERENCE OF THE EARTH CODED IN 12441.6 FEET.

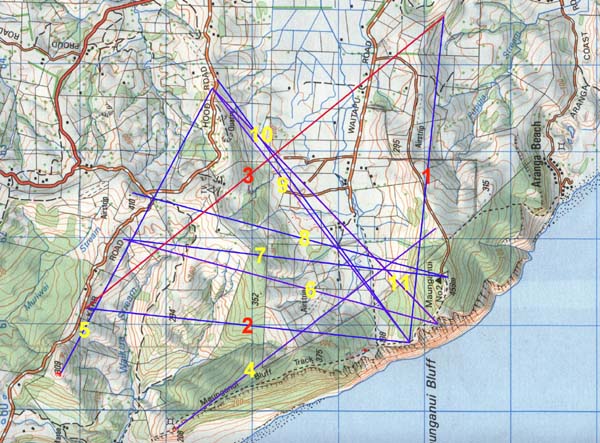
Figure 1: This picture demonstrates recurrences of the length 12441.6 feet in and beyond the Waitapu Valley. In each instance shown the length is running positively from marker to marker. In the case of the lengths numbered 1, 2 & 3 in the above picture, this is a right angled (isosceles) triangle with side values of 12441.6 feet and a hypotenuse that is, essentially, 17600 feet (to a shortfall tolerance of 59 inches). The 176 number was used copiously in ancient navigation and 1760 yards = 1 mile of 5280 feet. The reader is invited to thoroughly test the following concepts mathematically in order to understand the pedigree of the 12441.6 feet measurement. Let's start with the Greeks.

It is accepted that the most accurate measurements undertaken on the Greek Parthenon were those of Francis C Penrose in 1846. Penrose concluded that the width of the platform (stylobate), upon which the Greek temple is erected, measures 100 Greek feet.

Author Donald L Lenzen spent 10-years exhaustively assessing all known length increments, weight standards and volume vessels surviving in the Mediterranean Basin and wrote a book called, Ancient Metrology, based upon his research. Lenzen calls the Greek foot found by Francis C Penrose the,"New Greek Foot" and assigns it a value of 12.165 inches, based upon Penrose's measurement of the Parthenon platform. It is also officially accepted that there was a slightly shorter Greek foot that was 12.15 inches. Author John Michell speaks of a third type of Greek foot called the Samos foot of 12.096 inches.

The main "Greek" foot was a derivative of the "Stadium" and there were 600 Greek feet in a Stadium. At Olympia a "Stadium" length is marked in solid rock to indicate the start and finish lines for the Olympic running race. The length has been carefully measured at 630. 8 feet between the incised markers. This would most certainly have represented 630 feet, as the increment of 630 feet goes exactly 4.8 times into the base perimeter of the Great Pyramid. It is well known that the fledgling Greek empire got their measurement standards from the older Egyptian empire. If 630 feet indeed represents the length of a Stadium, then all of the Greek measurements make perfect sense. Eratosthenes said that the Greek mile was 8.33333 stadia (Stadiums), which would make it 5250 feet. This too makes perfect sense, as the increment is beautifully divisible by "7". The main Greek foot, therefore, was 12.6 inches or 1.05 feet.

Figure 2: Donald L Lenzen's drawing of the running track at Olympia. Incised marks into stone indicate the starting and finishing lines for the running event, which was over a distance of 630 feet of 12-inches, or 600 Greek feet of 12.6 inches

Added to and related to the above, there was a measurement of 34.56 feet found in the base paving slab region of the Great Pyramid that appeared to represent 20 slightly enlarged Egyptian Royal Cubits of 1.728 feet each (20.736 inches). Such a measurement increment would fit the base perimeter of the Great Pyramid perfectly (3024 feet = 1.728 X 1750). The same increment would have fitted the outer rim of the Sarsen Circle at Stonehenge perfectly, as it was regulated by a special PHI reduction of the Aubrey Circle diameter to be 110 feet (for a circumference of 345.6 feet). The PHI reduction on the Aubrey circle diameter went, 288 feet ÷ PHI = 178 feet (Y Holes diameter) ÷ PHI = 110 feet (Sarsen Circle diameter).

An increment of 3.456 feet (41.472 inches) appears to be very close to the Aztec Hunab found by Hugh Harleston at Teotihuacan and it's plausible to assume that one variety of Mayan/ Aztec Hunab was simply an Egyptian double Royal Cubit based upon a single Royal Cubit of 20.736 inches. Again, Harleston found slight variations in Hunab lengths that could not be attributed to poor or sloppy mathematical ability on the part of Teotihuacan's architects and builders. Like the Egyptians and Greeks, the Aztecs had very closely related, but marginally different increments to serve some purpose. Let's start with the largest set, which is a Hunab of 41.472 inches, an Egyptian Royal Cubit of 20.736 inches and a New Greek foot of 12.16512 inches (refined .00012" by this author).

After testing many GPS fixes within the exacting confines of AutoCAD, it is theorised that ancient New Zealand surveyor/ mathematicians were attempting to encode a length of 12441.6 feet between marked positions of the Waitapu Valley region. The double value of 12441.6 feet is 24883.2 and if this value were read as "miles" it would accurately represent the equatorial circumference of the world to a shortfall of only 18.8 miles on the official circumference value that we presently use.

Various scientists assessing the platform length (stylobate) of the Parthenon at Athens, Greece, have correctly postulated that it represented 1 second of Earth circumference arc. If the length is 100 New Greek feet of 12.16512 inches (101.376 feet), then this increment X 60 = 6082.56 feet (1 minute of arc) X 60 = 364953.6 feet (1-degree of arc) X 360 = 131383296 feet (convert to miles) ÷ 5280 = 24883.2 miles. This is 12 X 12 X 12 X 12 X 1.2 miles.

The use of this value (24883.2 miles) by the Greeks to describe the true equatorial circumference of the Earth is further corroborated by looking at the measurements used by the Egyptians, Mayans/ Aztecs and ancient inhabitants of Britain.

Ancient volume measures of the Mediterranean were fashioned in such a way that they would code some aspect of the "great knowledge" preserved and taught in the colleges. With this in mind, it's interesting to note that the largest Greek measure of capacity was the Medimnus @ 3110.4 cubic inches. This volume X 8 = 24883.2 cubic inches. The Greek Pygon length measurement, when cubed, equated to the capacity of a Medimnus. The Pygon was equivalent to the Egyptian Remen.

The reason is certainly not based upon the fact that the Greeks couldn't fabricate one standard ruler. Like the Egyptians, Mayans/ Aztecs and other cousin peoples, they had to make precise navigational calculations upon the open sea and consequently had to have fluid mathematical systems to facilitate positional plotting. Although the 24883.2-mile figure very adequately describes the true equatorial size of the Earth, it was the Great Pyramid standard that was used in navigation.

Whereas the length of the Parthenon platform is coded to be 1 second of arc in a true reading of the Earth's circumference, the full perimeter value of the Great Pyramid is 1/2 a minute of arc under a slightly different system. The perimeter value of the Great Pyramid is 3024 feet (756 feet per side) and if this represents 1/2 a minute of arc, then a second of arc is 100.8 feet, a minute of arc is 6048 feet and a degree of arc is 362880 feet. This culminates into an equatorial circumference read as 130636800 feet (24781.81818 miles). Interestingly enough the inner rim measurement across the Sarsen Circle at Stonehenge was 100.8 feet and the inch perimeter value of the Great Pyramid (@ 756 feet per side) is 36288 inches. So, let's explore the merits of the Great Pyramid's geodetic system and see how Greek measurements fit it.

The main Greek foot of 1.05 feet (12.6 inches) would go 124416000 times into 130636800 standard British feet. It will be recognised that this value is the same abbreviated numerical combination as that availing itself in the Waitapu Valley region of New Zealand (12441.6 feet...half of 24883.2).

The Greek Stadium of 630 feet would go 207360 times into 130636800 feet. It will be remembered that there was a slightly increased Egyptian Royal Cubit of 20.736 inches.

The Greek Mile of 5250 feet will go 24883.2 times into 130636800 feet.

The Greek foot spoken of by British author/ mathematician John Michell (1.008 feet or 12.096 inches), which he calls the Samos foot would go 129600000 times into 130636800 feet. The 12960 number and its doubled value at 25920 were used copiously in ancient cyclic mathematics, and 25920-years was used to describe the duration of the Precession of the Equinoxes.

The Greek foot of 12.15 inches (1.0125 feet) would also make perfect sense as a mnemonic device for making lunar calculations within the 6804-day lunar nutation cycle or the 2551.5-day period of the moon (7.2-lunar years) within the lunisolar Sabbatical Calendar system.

SO THE GREEK MEASUREMENTS WORK WITH THE EGYPTIAN GEODETIC SYSTEM, BUT HOW DOES THE MOST STANDARD EGYPTIAN ROYAL CUBIT FIT IN?

Figure 3: An Egyptian Royal Cubit from the Turin Museum collection has a published length value of 20.618 inches. With the Great Pyramid's base length set to 756 feet, 440 Egyptian Royal Cubits of 20.61818182 inches would equal 756 feet.

The Egyptian Royal Cubits were memory devices for remembering the size of the Earth under 3 main readings. We have already discussed the merits of the 20.736 Royal Cubit, which gives an equatorial circumference reading of 24883.2 miles. We'll now discuss two more slightly different Cubits.

Under a rule that applies to all 3.4.5 triangles the length of the adjacent is 1.66666666 less than that of the hypotenuse and the opposite is 1.25 less than that of the hypotenuse. If the base length of the Great Pyramid @ 756 feet were called the hypotenuse length of a 3,4,5 triangle, then it would produce an adjacent of 453.6 feet. This value (453.6 feet) is the vertical height of the Great Pyramid to the top of its flat altar floor (it's never had a capstone). Trigonometry dictates (given the pyramid's lengths and angles) that the top floor was designed to be 44 X 44 feet square.

Several formulas showed how to calculate the circumference of the Earth or 1-degree of arc, based upon the Great Pyramid's dimensions and angles.

You're not off the hook yet, as there's still one more cubit to discuss before we can go sailing.

The Great Pyramid was literally 756 feet long and complied to many increments of measurement within that length, which were based upon the numbers 6 & 7. Everything from Hebrew/ Celtic Royal Cubits of 21-inches and their "common" counterparts of 18 inches would fit snugly. Smaller fractions of the Greek Stadium and mile values fitted this length perfectly as well.

The British had a series of measurements that were based upon the number 11. The surviving lengths into modern times were the mile (5280 feet), furlong (660 feet), chain (66 feet), rod & perch (16.5 feet), fathom (earlier known to be 5.5 feet) and link (7.92 inches). Based upon ratio relationships between these values it becomes glaringly apparent that the ancient British league was 16500 feet (3.125-miles).

Although classicist historians might hold to the view that this "11" series only came into existence with the Tudor Monarchs (notably Queen Elizabeth the First), it is known that the 11 system is very old and measurements like the "chain" are traceable to ancient times. The Spanish, amongst others, have traditionally used measurement rods that were very close to 33-inches, like the Vara, which has survived until modern times in Spanish speaking countries. The Gaz of India is also very close to this value and was, undoubtedly, an "11" series measurement when first adopted from the universal parcel of standard increments thousands of years ago.

To work the "11" series on the Great Pyramid a symbolic adjustment had to be made to its length and 3 inches had to be added. This extra morsel was, undoubtedly, once marked into the base paving slabs, increasing the overall reading of the base perimeter from 3024 feet to 3025 feet. Now the pyramid complied to "11" series readings, as listed above. Under this length assignment (756.25 feet) it was 137.5 fathoms long.

Using the same logical sequence to produce an Earth circumference value under the "11" system we have:

It was seemingly essential for ancient navigators to measure their linear progress across oceans in terms of these "11" series values, hence the league or fathom have always been nautical terms. There's a very important reason for working in "11" series, straight line distances traveled, as they create very convenient relationships with the PI ratio (where a circle's circumference is always 3.1416 times larger than its diameter). One could, equally, work fluidly in "7" series increments, like the Greek mile of 5250 feet.

ZIG-ZAG TACKING YOUR WAY ACROSS THE WORLD, WHILE KEEPING TRACK OF WHERE YOU ARE AND WHERE YOU'RE GOING.

When sailing one is at the mercy of the wind to a large degree and must tack at angles to the breeze to make forward progress. The preferred course is not always achievable and tacking, first one way then another, is the only way to stay on course. It was the ominous responsibility of the navigators to always be aware of the ships position and distance from both point of departure or destination. The navigators had to be constantly aware of speed through the water and heading. Distances covered were measured in leagues, miles, furlongs or other increments of length within the "11" series of special navigational numbers (for a very profound reason).

When one counts off distances traveled in whole leagues, miles, furlongs or fathoms, then converts the completed linear distance to a circle, the circumference created will lend itself to accurate degree angle calibration. The navigators would maintain a vigilant watch on boat speed and from time to time feed out a knotted rope over the stern and count the time lapse between knots crossing the barrier aft. There would be tremendous cooperation between the helmsman and the navigator, who would work together to maintain the same course heading until a sought after distance had been traveled. The goal of the ever watchful navigator would be to complete segments of a voyage according to known distances and angles through multiple stages.

Let's now explore the ancient method for maintaining knowledge of the degree angle back to point of departure or onward to the final destination.

The strong prevailing wind is steady and allows for a straight line voyage. The navigator has the helmsman hold the course for a calculated distance of 23 leagues before angling the ship 15-degrees further to the northeast to take advantage of a wind shift. The navigator must now plot the newly completed, 23 league leg of the journey and calculate both the angle and distance of the ship from the port of Alexandria. He'll do this each time there's a significant change in the ship's heading.

The navigator goes to the plotting table and draws a line on the chart, scaled to represent 23 leagues. The line is set to the true angle trajectory around from north that the ship was on during the 23 league leg. This new line also connects to the previous line representing yesterday's distance covered and angle heading away from the port of Alexandria.

The navigator, using a scale ruler, sets his compass drawing tool to the scaled radius value of 23 leagues (11.5 leagues). He then uses the end point of the line (the ships present position on the sea chart) as the fulcrum to draw a perfect circle, which dissects the centre of the new line. The navigator knows that a circle based upon a diameter of 1-league (16500 feet) will produce a circumference reading of 51840 feet when using a very slightly modified form of PI @ 3.141818182. He knows that 1-degree of arc (1/360th) in a circle of 51840 feet is 144 feet. Because 23 leagues were traveled on the last leg of the voyage, the navigator knows that on this precisely scaled circle, each 3312 feet segment of the circumference represents 1-degree of arc. He duly adjusts his fine calipers by use of the scaled ruler to measure around from one of the primary points of the compass at N, S, E, or W and meticulously calculates the exact degree angle back to Alexandria. Using the same perfectly scaled circle, he can also see where the ship is presently headed, as well as the exact angle to the destination at Cornwall on the Isle of Cassiterides. The sum of 51840 feet, he knows, is also 30000 Egyptian Royal Cubits of 20.736 inches (1.728 feet).

The navigator reflects affectionately on the days when he was a raw initiate at the navigational school at the Giza Plateau and first learned the merits of the 51840 number. He well remembers how the old sage masters of the craft taught him that the Great Pyramid and Menkaure Pyramid had slope angles of 51.84-degrees, how the Great Pyramid's base covered 5184 square reeds of 10.5 feet each. He remembers learning that the area covered by the Great Pyramid's 4 faces and base equated to 51.84 pyramid acres of 28800 square feet each. The navigator reminisces about how he was taught the speed at which the earth rotates...let's see, how does that go again...24883.2 miles of true circumference divided by 24 hours = 1036.8 miles per hour (518.4 X 2). Yes indeed, he muses quietly to himself, the 5184 number has certainly come in handy for many generations of my cousin people and is guaranteed to get this ship safely to the tin mines of Cassiterides beyond the pillars of Hercules.

On day four of the voyage the Mediterranean mistral wind rises and the ship can't maintain the heading to complete an anticipated 15 league leg, but is forced to tack onto a new heading early. The adept helmsman manages to maintain the angle until a calculated distance of 45 miles are covered. The navigator thanks the helmsman for holding the course so skillfully, assigns the new heading, then proceeds to the plotting table. This calculation will have to be in miles and the navigator draws a scaled down 45 mile line, on the correct angle, across the chart. Again, he goes to the end position of the line and draws an accurate circle with his compass tool. From memory the navigator knows that a diameter of 5280 feet produces a circle of 16588.8 feet, which is also 9600 Egyptian Royal Cubits of 20.736 inches (1.728 feet). This means that 1-degree of arc is 46.08 feet or 11.52 feet X 4. He duly calculates that the 45 mile diameter circle produces a circumference wherein each degree of arc is 2073.6 feet or 11.52 feet X 180. Again the angle back to Alexandria is calculated with ease.

As he dwells upon working once again with the 1152 number, the navigator remembers anew his days as a student on the Giza Plateau. He recalls how the old teachers demonstrated that the Menkaure Pyramid covered an area of 11.52 pyramid acres of 28800 square feet for its four faces and base under its PHI length assignment of 356 feet. He remembered learning how each face of the Great Pyramid was 230400 square feet (115200 square feet X 2) or 8 Egyptian pyramid acres. Yes indeed, the 1152 family of numbers had served his people well since before anyone could remember and has helped them at sea yet again today.

Beyond the pillars of Hercules the ship encounters a heavy Atlantic current that pulls to the south and it's difficult to make headway to the northeast. Progress for a leg is limited to just over 3 miles until the ship can get clear of the rip. The navigator calculates that the conditions have allowed them to move only 26 furlongs or 17160 feet. Being a methodical stickler for detail and knowing that small discrepancies in plotting can accumulate into large discrepancies, the navigator heads to his plotting table to record the paltry leg. He knows that a straight line diameter of one furlong will produce a circumference of 2073.6 feet or 24883.2 inches, which is 1200 Egyptian Royal Cubits of 20.736 inches (1.728 feet). With a dismal 26 furlongs having been covered, each degree of arc on the final drawn circle is 5931.39 feet or 1152 feet X 46.8. The southern end of Cassiterides is coming into view on the horizon and from here on landmarks will be available if the traditional and all too frequent mists of the region stay away. Being this close to land in the unpredictable Atlantic is fraught with danger and everyone will have to stay alert. If conditions deteriorated markedly the navigator will have the ship turn to the open sea, then guide them back to the port of destination in more predictable and controllable circumstances. The lives of the entire crew, as well as their precious cargo, are in the hands of the navigator and this sobering thought is forever on his mind. He has the size of the Earth and how to grid reference it for successful navigation locked into his memory. The sea, he knows from long experience, does not abide fools well, nor forgive them for their lack of training. Thankfully, he was trained by the best.

Some things can sit eternally at the back of the mind. They constitute a part of the overall navigational training, but are rarely, if ever used. The navigator knows he can plot according to the small increment of a fathom of 5.5 feet, which diameter will produce a circumference of 17.28 feet or 10 Egyptian Royal Cubits of 20.736 inches. The only time he'd had to use fathoms was to navigate himself back to his ship when Zorba the Greek navigator had cracked an amphora and plied him with a little too much of a very palatable Aegean elixir. As the navigator vaguely recalled, he and Zorba had argued about the best increments for navigation, as the Greeks used their own "7" based version within the old navigational system. The two of them would have touched upon the alluring beauty of Irene Papas, but she wouldn't be born for several thousand years yet.

The Greeks had a series of "7" based increments, which ranged from the Greek foot of 12.6 inches to a stadium of 630 feet and a Greek mile of 5250 feet. From this we can deduce that they also used the Hebrew reed of 10.5 feet, as well as the Hebrew Royal Cubit of 21-inches, all of which values fit the base dimensions of the Great Pyramid perfectly.

Erastosthenes tells us that the Greek mile was 8.33333 stadia. Inasmuch as the stadium measurement, was originally based upon Great Pyramid values and configured to be 630 feet, this can only mean an increment of 5250 feet or 500 reeds. It is evident that the Greeks had in their possession the entire system of increments (6, 7, 11 & PHI based) that their cousin peoples of the Mediterranean and Europe shared, but might have had a particular preference for "7" based progressions in general measurement.

The "7" based equivalent to the "11" based, 5280 feet mile is the Greek mile of 5250 feet. The Greek equivalent to the 660 feet furlong was the 630 feet stadium. Let's go sailing using the Greek "7" system, which also functioned perfectly for lunar and Sabbatical calendar calculations.

Again, we're using the Great Pyramid standard for the navigational and grid referencing size of the Earth, wherein 3024 feet = 1/2 a minute of arc for the world. Another way of arriving at the the Great Pyramid's full Earth size figure is to multiply 3024 feet X 43200 = 130636800 feet or 24741.81818 miles. This figure is 24883.2 Greek miles of 5250 feet.

Zorba the Greek navigator is aboard a ship transporting bronze, ox-hide shaped ingots to the Aegean Sea and the crew have been able to maintain an undeviating course for a calculated 58 Greek miles (304500 British feet or 290000 Greek feet of 12.6 inches each). A wind shift then necessitates that the ship change its heading and Zorba the navigator goes to his plotting table to record this last successful leg of the journey. He knows that a Greek mile diameter of 5250 feet produces a circumference of 16500 feet (an ancient British league) when subjected to a "7" based PI rendition of 3.142857143 (22/7ths). This circumference value is 9600 Egyptian Royal Cubits of 20.625 inches. Under this system, 1-degree of arc on a circle of 16500 feet is 550 inches or 8.333333 fathoms of 66 inches each. Zorba takes his compass tool and draws a precise circle at the end of his scaled chart line, which represents a diameter traveled of 58 Greek Miles. By calculation he ascertains that each interval of 2658.33333 feet represents a degree of arc and calculates the angle back to the home port, as well as to the ship's destination without difficulty.

One leg of the journey on the approach to Cape Gelidonya falls short of 16 Greek miles and it is decided to calculate the distance in stadia of 630 feet. The overall distance traveled is estimated by Zorba to be 130 stadia or 81900 feet. Zorba knows that the circumference produced from a diameter of 630 feet is 1980 feet or 3 furlongs. This circumference complies to 1152 Egyptian Royal Cubits of 20.625 inches each and one degree of arc is 5.5 feet or 1 British fathom. Inasmuch as 130 stadia constitute the diameter of the circle, Zorba knows that every 130 fathoms represents 1 degree of arc.

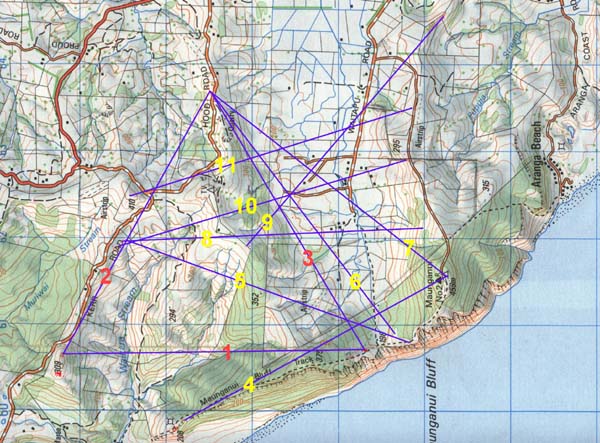
Figure 4: The picture shows recurrences of the 11520 feet length running accurately between markers. Lengths 1, 2 & 3 form an equilateral triangle, with side 3 angled at 59.0625-degrees (59.0625-days is two lunar months). The length up the side of Khafre Pyramid is 590.625-feet. Identifiable codes also reside in the angles running between many markers. In future articles the codes contained in each of the above lines and angles will be discussed.

Anyone using the Greek "7" based navigational system would be constantly encountering the numbers that occur when tracking the 6804-day cycle of the moon or incremental values within the Sabbatical calendar system. For this reason it's a wonderful integrated system, wherein the mariner constantly had at hand all of the information necessary to do calendar counts and predict weather patterns (in consideration of the moon's known crossing orbit).

Many thousands of years ago cousin peoples from the Mediterranean and Europe sailed to far distant isles at the end of the world and set up colonies. With them they brought their profound astronomical and navigational sciences and, lest it be forgotten, encoded the age-old principles into the landscape. For thousands of years these enlightened people prospered peacefully at the far ends of the Earth, until the coming of the warriors who eventually annihilated them. That such a misfortune overcame them is very sad and tragic, but it's a common enough occurrence from continent to continent, where thriving civilisations have oftimes met an untimely demise.

One would think that brutal annihilation was more than sufficient to warrant no further insult to the ancient inhabitants of these islands, but that, sadly, has not been the case. Factions within New Zealand zealously stop any knowledge, related to the former long-term population, coming into the public sector. These factions hide or suppress skeletal evidence, ancient scripts/ pictograms incised into stone and anomalous artefacts that would shed light on who, exactly, the core population was. Most traditional art forms and symbols found within Maori culture were acquired from the earlier civilisation.

Public officials, whose wages are paid from the public purse, are deceitfully engaged in using their positions to hide true history from New Zealanders. The ancient people are not allowed to be remembered.

This impasse is most unfortunate, nevertheless the ancient people are still empowered to "speak to us from the dust". The cairn, standing stone and mound marker systems that they left in the Waitapu Valley still remain as guardians of the ancient sciences and, with a little rousing, can be stirred and awakened from a long period of dormancy. Although the voices of the learned Masters of the Craft have fallen silent, much of their encoded knowledge remains intact and can be restored. The age-old sages imparted their enlightened "sciences of civilisation" and "philosophies of harmony" to countless generations of initiates, through the worldwide distribution of schools, prior to the Christian era. If they could speak to us today, I think they would say: