THE CODED DISTANCES & ANGLES OF THE HORSESHOE'S HUB POSITION, TO OTHER STATIONS WITHIN THE OCTAGON COMPLEX
We have already seen
that the hub position of the small horseshoe embankment is tied by exacting
geometry to the two main hub positions of the greater Octagon site, but that's
only the beginning... Let's now identify how the horseshoe further preserves
a raft of ancient codes by virtue of its position. We'll start off with some
easy ones and then introduce more complex codes later.
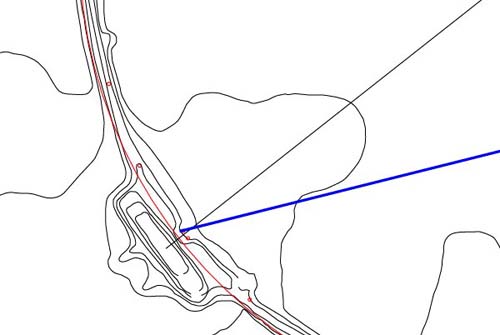
Figure 46: The blue
line originates at the hub position of the small horseshoe embankment and
extends for 1980 feet to a very significant shelf at the forefront of the
altar. The azimuth angle of this line is 256-degrees.
- 1980 feet is 1/4th
of 7920 feet and the number 7920 was used to describe the diameter of the
Earth in miles. Under the "11" series Earth navigational system the Earth's
circumference was considered to be 7920 leagues of 16500 feet each (3.125
miles, 25 furlongs, 250 chains, 1000 rods/ perches, 3000 fathoms or 25000
links).
- The distance of 1980
feet is 360 fathoms and this distance is 1/66000th of the circumference of
the Earth under the "11" series geodetic system, which worked to 24750 miles
for the ring of the Earth.
- The angle of 256-degrees
codes "256", which was an important value in a geodetic mathematical progression,
based upon 8, 16, 32, 64...etc. The progression produces numbers like 2304
(solar and navigational).
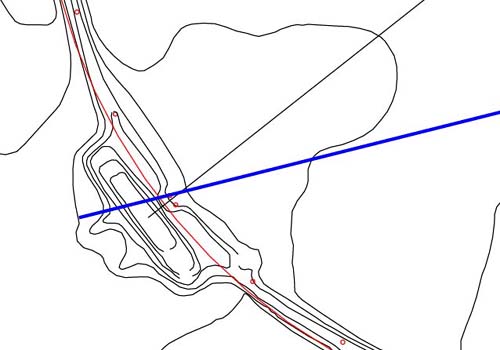
Figure 47: This distance
from the horseshoe hub to the extreme outer position of the altar is of extreme
importance, as in its inch count it divulges the exact circumference of the
Earth under the sexagesimal navigational system. This distance is exactly
1200 Egyptian Royal Cubits of 20.61818182 inches each. Note how the vector
tucks into the corner position adjacent to "horns" of the altar.
- Under the sexagesimal
geodetic system the height of the Great Pyramid was read as 453.6 feet.
- To find the size of
the Earth, this number was divided by 1/2 the length of the Pyramid's flat
floor top (or 22 feet).
- The resultant value
was 453.6 ÷ 22 = 20.61818182 feet. This number could then be read as
247.4181818 inches and the size of the Earth was, under the sexagesimal system,
24741.181818 miles in circumference.
- Generally, mnemonic
rods were fabricated that were 20.61818182 inches long and when this figure
was multiplied by 1200 the value produced was read as miles...thus 20.61818182
X 1200 = 24741.181818 miles.
- The same principle
is demonstrated by this vector originating at the horseshoe hub, which extends
for 1200 Egyptian Royal Cubits or 2061.818182 feet (24741.181818 inches)...with
each inch representing a mile of the Earth's circumference.
- To find the sexagesimal
size of the Earth by an altogether different method, simply multiply the perimeter
value of the Great Pyramid (3024 feet) X 43200 (a sun radius value) = 130636800
feet... then convert this to miles (divided by 5280) = 24741.181818 miles.
- To find one degree
of arc for the world (in miles) under the sexagesimal geodetic system, simply
divide the length of the Great Pyramid by 11 and read the total as miles...756
÷ 11 = 68.727272 (miles).
- Again, the azimuth
angle used is 256-degrees...an 8 numerical progression.
Let's move from the altar,
having only partially demonstrated the latent codes residing there. Our purpose,
for the moment, shall be to cover a wide selection of outpost stations, all
over the site and show how they relate, in code, to the small horseshoe circle.
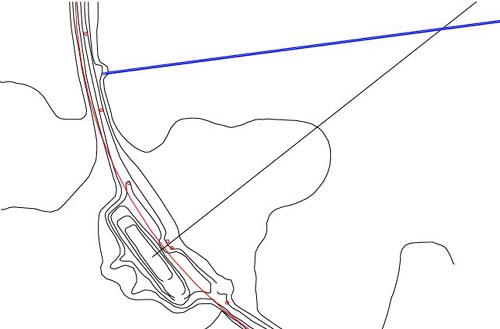
Figure 48: Around
the circle embankment, the ancient architects created conspicuous positions
that stood out very obviously as places of significance. In the above picture
is a jutting hump peninsula that almost cries out for recognition. The blue
line extending from the horseshoe hub to this hump is 2016 feet long and is
on an azimuth angle of 262.5-degrees. Both the distance & angle codes being
demonstrated are very dynamic.
- The flat floor altar
atop the Great Pyramid worked to two coded values, the inner of which was
42 feet per side.
- The sum total of all
4 sides of the altar, under this calibration, was 168 feet or 2016 inches
and this number, based upon 42, is very important to many general applications
of ancient astronomy.
- The distance of 2016
feet also equates to 1152 Celtic Royal Cubits of 21 inches each and this increment
(2016 feet or 1152 Royal Celtic Cubits) offered an alternative means of reading
the size of the Earth under the sexagesimal system.
- By this system, the
Earth was 64800 increments of 2016 feet, with 1 degree equating to 180 X 2016
feet & 1 minute of arc to 3 X 2016 feet...with a second of arc representing
.05 of 2016 feet.
- The distance of 2016
feet is also 192 reeds.
- The azimuth angle
is 262.5-degrees and this related in a dynamic way to the lunar nutation cycle.
It is also related to the reed measurement (10.5 feet) and 2.625 feet is 1/4th
of a reed. At Stonehenge every 26.25 feet (2.5 Lintels) represented 12-degrees
of arc on the inner rim of the Sarsen Circle.
- The Serpent Mound
in Adam's County Ohio is 525 feet from the tip of the tail to the pyramidal
apex at the forward extremity of the head...or 262.5 feet X 2.

Figure 49: Another
obvious jutting hump built into the Octagon's circle. Both a circle & vector
are sent out from the hub of the horseshoe circle and the circle tucks into
the corner of the hump on both sides of the embankment. At the same time the
vector points directly toward the nose of the hump. The circle has a radius
of 1417.5 feet or a diameter of 2835 feet. The azimuth angle of the vector
is 283.5-degrees and this is one of the foremost of the lunar codes.
- From the shelf, forward
of the altar, to the furthest extremity of the Octagon, the distance was coded
to be 2835 feet.
- The perimeter value
of Khafre Pyramid @ 708.75 feet per side = 2835 feet.
- 1/24th of the lunar
nutation cycle was 283.5 days and this time period was also 9.6 synodic lunar
months of 29.53125 days each.
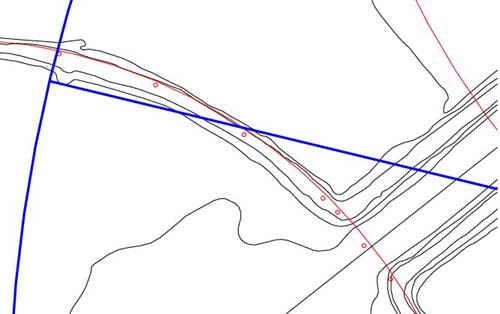
Figure 50: Another
extremely significant code, associated to the "hump", is shown by the circle
rim 1440 feet out from the horseshoe hub. Note how the 1440 feet radius circle
tucks into the opposite corner to the 1417.5 feet circle shown earlier. Again
the azimuth angle is 283.5-degrees, in deference to the major lunar code and
the perimeter of the Khafre Pyramid. Note how the 283.5-degree vector brushes
the nose of the hump.
- The 1440 feet radius
(2880 feet diameter) is a major ancient code, with the 288 number featuring
as, arguably, the most important base number of antiquity...alongside 11.52,
51.84 & 25920, which are all related within the selfsame mathematical progressions
anyway.
- The court altar of
the Temple of Solomon was 1440 inches in perimeter value.
- The Aubrey Circle
at Stonehenge was 144 feet in radius value.
- There were 21 increments
of 144 feet in the perimeter value of the Great Pyramid.
- The ancient Egyptian
acre (pyramid acre), as identified by Herodotus, was 28800 square feet.
- The overall, defining
length of the Octagon, from the rear alcove of the Altar SW, to the outer
line of the gateway NE is 2880 feet.
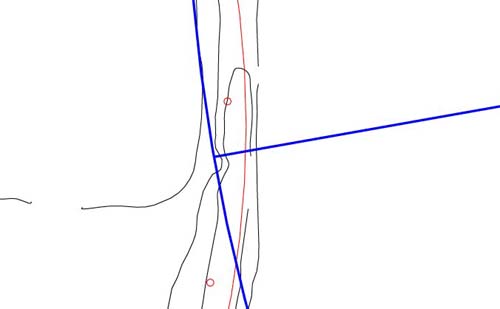
Figure 51: Another
deliberate indentation marking of the circle embankment occurs at 1000 feet
out, at an azimuth angle of 260 degrees, from the horseshoe hub. The merits
of having a decimalised distance of 1000 feet are self- explanatory. The 260-degree
azimuth coded Sabbatical calendar increments, as well as symbolically represented
259.20-degrees (precession).
- Under the Sabbatical
calendar system there were 52 weeks in a year or 26 weeks from equinox to
equinox.
- The Sabbatical system
was based upon a year of 13 months, each of 28 days duration (364 days).
- The system worked
in increments of 13 through to the Sabbatical year when calendar corrections
were made (8.75 days of accrued deficit).
- The "13" based system
continued to work through to the Jubilee year, just prior to which final corrections
were made to render the calendar absolutely precise before venturing into
another 50 year solar cycle.
- The Sabbatical calendar
system is encoded into the funeral mask of Tutankhamun.
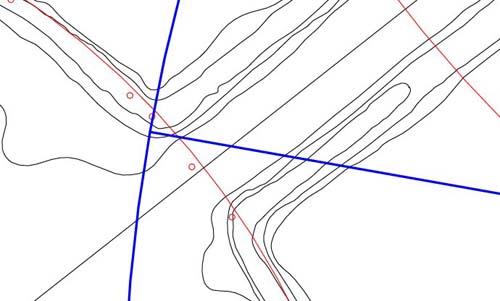
Figure 52: An important
coding of the corner position leading into the Avenue. This distance is 1134
feet radius from the hub of the small horseshoe circle or on a circle of 2268
feet diameter. Such a circle would be 3/4ths of the perimeter value of the
Great Pyramid @ 756 feet per side. The number is also a very prominent lunar
code, much accentuated at Stonehenge. The azimuth angle from the horseshoe
hub to this position is exactly 280-degrees, an important value in both solar
and lunar counts under the Sabbatical calendar or lunar nutation cycle systems.
- At Stonehenge the
Station Stones rectangle measures 264 feet X 113.4 feet.
- The slightly elliptical
Sarsen Circle at Stonehenge achieves its greatest width on an azimuth of 45-degrees
to 225-degrees...and this width (outer face to outer face) was designed by
its architects to achieve 113.4 feet.
- The value of 113.4
days would be 1/60th of the lunar nutation period, spanning 6804 days .
- One of the defining
circles for fixing the hub position of the horseshoe circle has a diameter
of 1701 feet (lunar code). The sum of 1701 is, simply, 1134 X 1.5.
- The azimuth angle
code @ 280-degrees is reminiscent of breaking the 6804 day lunar nutation
cycle into 28 periods of 243 days...a value much in evidence at Stonehenge.
- Both solar & lunar
counts were done using the 56 posts of Stonehenge's Aubrey Circle...56 = 2
X 28.
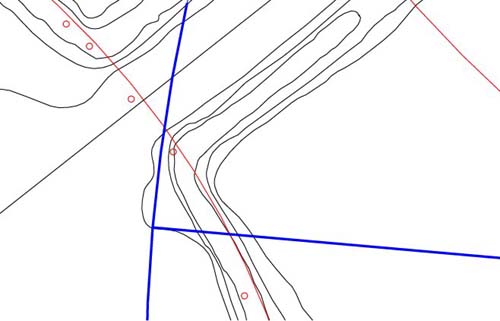
Figure 53: There are
a number of codes resident in this corner position, some of which are a little
complex. This circle extends out from the horseshoe hub a radius distance
of 1080 feet and the vector accompanying it is on an azimuth angle of 275-degrees.
Note how the vector brushes the side edge of elevated ground south of the
embankment corner, while the circle runs through a forward section of the
lower corner.
- The numerical value
1080 was much used in ancient astronomical mathematics. A calibration assigned
to the Aubrey Circle at Stonehenge was 900 feet of circumference, or 10800
inches. The sum of 1080 feet is exactly 400 rounded Megalithic Yards of 32.4
inches each.
- A mathematical progression,
based upon 108, delivers up many of the most important numbers of antiquity
in all categories of solar, lunar and navigation, all the way up to the size
of the Earth under its sexagesimal assignment.
- The azimuth angle
of 275-degrees is half of 550 and this vector codes the most primary navigational
system, which used an "11" series linear distance to create a sexagesimal
circumference.
- An example of why
1080 & 275-degrees would have been coded together stems from the fact that
a 275 radius produces a 1728 circle, which is 108 X 16. This mathematical
principle would have featured prominently in navigation for determining degree
angles.
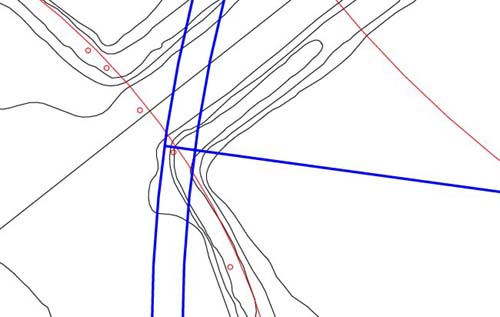
Figure 54: The best
representation of the exterior corner position resides at the seemingly strange
azimuth angle of 277.777-degrees. At the same time 1080 feet distance from
the horseshoe hub works effectively to designate the outer corner position.
Also shown is a more inward circle sweeping to the inner line of the highest
layer of the embankment. This second circle has a radius of 1056 feet, which
is the same as the crest-to-crest distance across the Octagon's circle embankment
(ref. James A. Marshall).
- The seemingly strange
azimuth angle of 277.777-degrees is a code for breaking a 360-degree circle
up into increments related to the Precession of the equinoxes...thus 360-degrees
divided by 277.77777 = 1.296 (precession endured for 25920 years, which is
12960 X 2).
- On 4 points of the
Octagon site the exterior limits of the gateways fit within a circle of 1485
feet or 550 rounded MY. Under the navigational rendition of PI of 3.141818182,
this diameter produces an encasing circle for the 8 embankments of 4665.6
feet, which is 12.96 feet per degree of arc.
- The number 277.777777
is 1/9th of 2500.
- When the Great Pyramid's
inch perimeter value (36288 inches) is divided by 277.7777777, the achieved
result is 130.6368 inches. This value, if multiplied by 12 million, would
represent the circumference size of the Earth under its sexagesimal navigational
assignment... 130636800 feet or 24741.81818 miles. The same breakdown formula
applies to the Great Pyramid under its "11" series inch assignment (36300
inches), wherein the globe was considered to be 24750 miles (7920 leagues)
in circumference.
- The 1056 feet distance
from the hub of the horseshoe is 1/5th of a mile and this same distance was
used as a primary calibration circuit at Stonehenge for 3,4,5 triangulation
measurements onto the embankment there. At Stonehenge the 1056 feet of circuit
was used for determining the alighting positions of stars and planets, as
seen from a central point of observation, with each 1.76 inches (mile progression)
representing 1/2 a degree of azimuth arc.
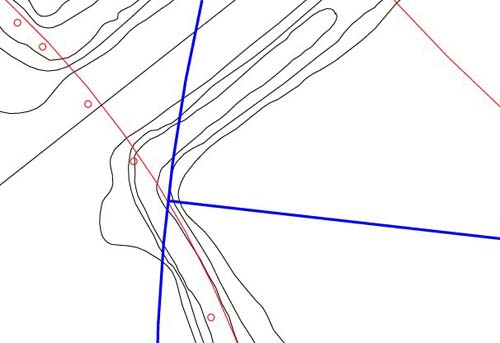
Figure 55: The circle
edge, in this case, is 1050 feet (100 reeds) from the hub of the horseshoe.
One of the coded circles used within the circle embankment of the Octagon
was, assuredly, 1050 feet.
It's possible that the azimuth angle of 276.48-degrees was used to describe
this inner corner position. The number has an association to a calibration
used on the altar floor of the Great Pyramid, based upon a circle of 44 feet
diameter, producing a circumference of 138.24 feet or 12 segments of 11.52
feet each. The increment of 276.48 inches would have been 1/6th of the altar's
calibration circuit. The altar's circuit was designed to represent 1/945000th
of the size of the Earth under the sexagesimal assignment and its important
defining number 138.24 X 2 = 276.48.

Figure 56: The Avenue
codes to the left hand side at the entry to the octagonal component of the
greater site. The exterior position complies with a distance of 990 feet from
the horseshoe hub, whereas 960 feet would describe a position on the rising
interior corner. The azimuth angle of the vector shown is 293.3333-degrees.
- The distance of 990
feet is 180 fathoms or 11/2 furlongs (there are 960 fathoms or 8 furlongs
per mile).
- The distance of 990
feet represents 132000th of the circumference of the Earth under the "11"
series geodetic system.
- The more inward distance
of 960 feet is 11520 inches and there are 960 fathoms in a mile...or 5.5 increments
of 960 feet in a mile.
- The azimuth angle
@ 293.333333-degrees represents a mathematical progression within the "11"
series geodetic system of navigation and produces numbers associated with
the mile & league...880, 5280, 7920, etc.
- At Stonehenge the
embankment circle crest was 1056 feet in circumference or 2.9333333 feet per
degree of arc (35.2 inches per degree or 17.6 per 1/2 degree).

Figure 57: The vector
running to the right hand side of the Avenue is on a seemingly strange angle
of 291.111-degrees from the horseshoe hub. The corner position is 900 feet
removed. This important vector extends across the Avenue to the nose of the
crest hump atop the embankment. The opposite running angle back to the horseshoe
was 111.111-degrees and this angle provided a very important conversion ratio
used for mnemonic recall of many ancient codes.
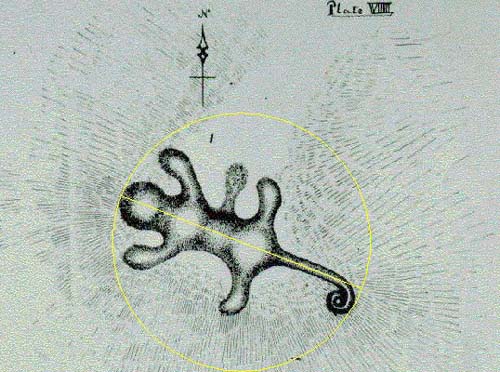
Figure 58: The "Alligator"
Mound, a few miles west from Newark's earthworks. The picture shown, minus
the added geometry, was drawn by James A Salisbury, circa 1862 and labelled
by him as Panther Mound. The official length of the mound appears, plausibly,
to be 210 feet (1/3rd of a Greek stadia of 630 feet).
Its centre line appears to lie on an angle of 111.111-degrees, from the centre
head section down the line of the tail. This degree angle codes an important
ratio in common usage amongst ancient astronomer/ mathematicians. Salisbury's
drawing is considered to be the most accurate depiction of the Alligator Mound
available.
More stringent checking will be required to establish the validity of this
degree angle at Alligator Mound and either 110 or 112-degrees would also fall
within the parcel of ancient coded values.
- Some examples of how
1.111111 was used would include...25920 (precession) X 1.11111 = 28800 (the
sq. footage in an Egyptian or pyramid acre), 6804 (lunar nutation cycle) X
1.111111 = 7560 (the length of the Great Pyramid was 756 feet), 472.5 (Khafre
Pyramid height) X 1.111111 = 525 (the reed measurement was 10.5 feet or 5.25
feet X 2). 356.4 (Menkaure Pyramid length) X 1.111111 = 396 (1/2 of 792...the
Earth is 7920 miles wide and was anciently calibrated to 7920 leagues circumference
under the "league" geodetic system). Alternatively, expanded ratios like 2.222222
or 3.333333 were used.
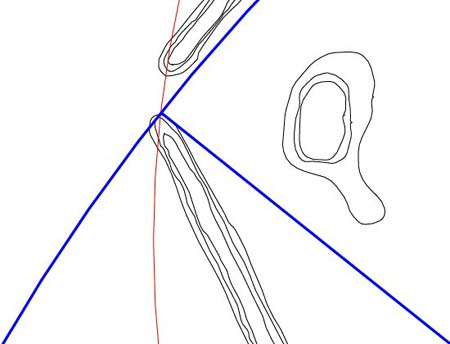
Figure 59: The blue
circle shown extends out 1440 feet from the horseshoe hub on an azimuth angle
of 308.5714286-degrees. This complicated degree angle is, very simply, an
expression of dividing 360 degrees into increments of 7 and 308.5714286-degrees
represents 6/7ths of 360-degrees. As strange as it might seem, ancient astronomer/
mathematicians often divided circumferences up into 7th increments, primarily
for calendar calculations and had a very simple system for working with the
cumbersome numbers generated.
- The court altar of
the Temple of Solomon had a perimeter value of 1440 inches and this number
(especially doubled out to 288, 2880, etc.) is a foundation number upon which
ancient astronomical methodology is built.
- The Aubrey Circle
at Stonehenge has a radius of 144 feet. The Menkaure Pyramid had an intended
face diagonal length of 288 feet.
- The Octagon's defining
length is 2880 feet.
- The Great Pyramid
had a face diagonal length of 576 feet (144 X 4) and a face square footage
value of 8 Egyptian acres per side (Herodotus)...of 28800 sq. feet each.
- The geomancer's mile
of Great Britain was 14400 feet.
- This 1440 feet circle
at the Octagon also cuts through the northern pillar marker position of the
Octagon's circle embankment
- In Britain the number
144, from longstanding tradition, determined the "gross" weight.
The Brasen Sea edifice in the court of the Temple of Solomon was circular
and had a rim value of 630 inches (5 reeds). It was very obviously set up
to this calibration so that it could work in increments of "7" and be used
for calendar day counts, within the Sabbatical cycle system.
When one wishes to break 360-degrees into "7" based increments, the numbers
generated are complex, unless the rim value is specifically sized to work
to "7".
The ancient mathematicians used the ratio 1.75 and the length 630 when working
in "7" numerical values. A "7" based circle would comply with a value directly
founded on 630, (7 X 90) or a related progression. One could convert angles
within the 630 circuit to sexagesimal values within a 360 circuit, by dividing
by 1.75.
- On the Brasen Sea
edifice of the Temple of Solomon the rim position, at 540 inches, represented
6/7ths of the rim total.
- This position (540
inches) divided by 1.75 = 308.5714286-degrees.
- The Menkaure Pyramid
of the Giza Plateau is, in its assigned coding, exactly 1.75 in ratio less
in base perimeter value than the Dashur Pyramid at Saqqarah (officially 190
metres square...623.35958 feet...should be read as 623.7 feet) This value
(623.7 feet) divided by 1.75 = 356.4 feet (Menkaure). The difference between
the two base assignments is that Menkaure is built to 356.4 feet & Dashur
to 356.4 Royal Celtic Cubits of 21 inches each.
- A major calibration
circle at Stonehenge, extending from site centre to a small post circle epicentre,
situated on the Avenue, has a radius of 175 feet.
- The ratio difference
between the Great Pyramid's base perimeter (3024 feet) and that of Silbury
Hill in Southern England (1728 feet) is 1.75 to 1.
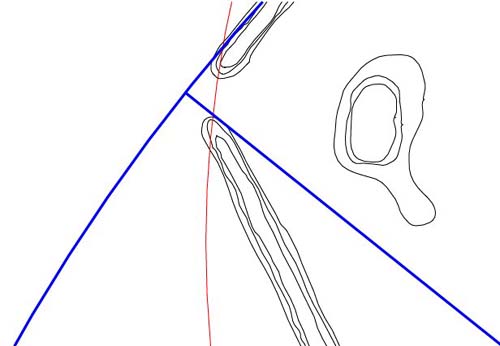
Figure 60: This vector
length, extending for 1466.666666 feet from the hub of the horseshoe was undoubtedly
included in the coding, as it pertains to navigation under the "11" series
system. We've already covered the merits of 293.333333 and 1/2 that value
is 146.666666...relating to 880, 5280, 7920, etc.
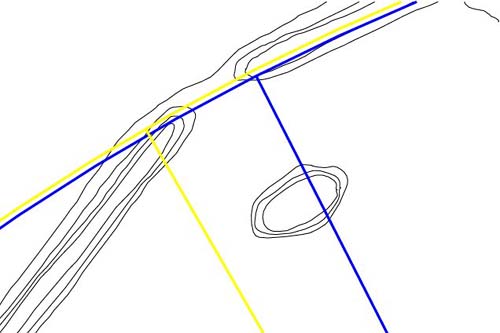
Figure 61: The PI gateway,
where coding in both the PI ratio and the Greek stadia measurement were accentuated
simultaneously. The blue circle is 1570.8 feet from the hub of the horseshoe
circle and this is indicative of 1/2 PI (1.5708). This means that the full
diameter circle would be 3141.6 feet wide (PI is 3.1416).
Note how the blue circle
relates with the centre nose of the left bank.
The yellow circle is 1575 feet from the horseshoe hub, for an overall circle
diameter of 3150 feet (5 Greek stadia). Note how it interrelates with the
centre nose of the bank to the right. Two vectors (one blue and one yellow)
extend to this area. The blue one has an azimuth of 333.333333-degrees or
a ratio of 1 to 1.08 of a circle of 360-degrees. The yellow one has an azimuth
of 330-degrees and was probable marked out within the Octagon, inasmuch as
it is so important to the "11" series geodetic system, as well as the furlong
(660 feet and the chain (66 feet).
- The Greek Stadia measurement,
in its half value (315 feet), was designed to represent PI symbolically, while
working in the "7" based numbers associated with the reed measurement (10.5
feet) or Celtic Royal Cubit (21 inches). All such measurements originated
in pre-dynastic Egypt and were carried westward by late era migrants (about
4000BC). The pyramids are many thousands of years older than the dynastic
period of Egypt.
- The inner rim of the
Sarsen Circle was read as 314.16 feet & 315 feet simultaneously, to represent
PI as well as 1/2 a Greek stadia, 30 reeds, 180 Royal Celtic Cubits and 3780
inches (Great Pyramid).
- The Great Pyramid
is 4.8 stadia in perimeter value.
- The Khafre Pyramid
is 4.5 stadia in perimeter value.
- The 8 embankments
of the Octagon & marginal extensions of them into the gateways, were used
on the basis of 1 Greek stadia or 630 feet each, for a total perimeter value
of 8 stadia or 5040 feet. Note: one of two calibrations assigned to the altar
atop the Great Pyramid worked to 504 inches per side. The combined total of
5040 feet, represented in the 8 Octagon embankments, is 1/25920th of the size
of the Earth under the sexagesimal navigational system. The duration of the
Precession of the equinoxes was anciently calculated to be 25920 years.
- The sum of 5040 feet
is also 2880 Royal Celtic Cubits, 60480 inches (the Great Pyramid was 3024
feet in perimeter, which is 6048 feet divided by 2), as well as 1.35 minutes
of azimuth arc for the ring of the Earth.
- PI coding is strongly
represented at Stonehenge, as well as within the former Crosshouse at Miringa
te Kakara in New Zealand (one of the few ancient meeting houses, built to
Northern Hemisphere astronomical codes, to survive into the late 20th century).

Figure 62: Very important
codes reside in the northern gateway, which relate, primarily, to 3,4,5 triangulation,
the league measurement or the size of the Earth under both the sexagesimal
and "11" series geodetic systems.
- The blue circle is
1666.6666 feet from the hub of the horseshoe and this value was designed to
code a principle of 3,4,5 triangulation, wherein the "adjacent" is always
1.666666 less in value than the "hypotenuse". Alternatively, the "opposite"
is always 1.25 less in value than the "hypotenuse".
- It will be remembered
that a most outward limit-defining circle for the octagonal component of the
site was 1485 feet (550 rounded MY). This value (1485 feet) X 1.666666 = 2475
feet. The ring of the Earth under the "11" series geodetic system was 24750
miles.
- The blue vector extending
for 1666.6666 feet lies on an azimuth angle of 353.454545-degrees. This is
1/70th of 24741.81818 (the number of miles in the ring of the Earth under
the sexagesimal system).
- The yellow circle
is 1650 feet from the hub of the horseshoe and this value is related to the
league measurement. The 1650 feet equates to 1/10th of a league, as well as
2.5 furlongs, 25 chains, 100 rods/ perches, 300 fathoms and 2500 links.
- The yellow vector
lies on an azimuth of 353.5714286-degrees, which is 1/70th of 24750 (the "11"
series size of the Earth in miles). Remember that 1/7th expressions like this
could be easily dealt with by use of the 1.75 ratio, which made them divisible
by 9 or 90.
- Note how the blue
vector brushes the inner mound en route to its station and how the yellow
vector relates to the nose of the right embankment.
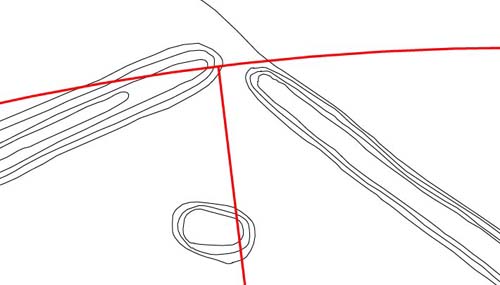
Figure 63: This is
a probable code, under the assumption that, "if this researcher can find it,
then the ancient astronomers were probably aware of it". As we proceed, it
will be demonstrated that an alignment of 38.88-degrees azimuth runs down
the ESE embankment to the hub position of the horseshoe. The horseshoe position
is, therefore anchored to 38.88 degrees, which is a part of a precessional
progression, based upon 12.96-degree increases.
If we accept that 38.88-degrees represents a zero or beginning point, then
the red vector shown above represents 314.16 degrees of increase (PI coding)
on 38.88-degrees and sits at an azimuth of 353.04-degrees. Again, the red
circle aspect codes 1650 feet and relates to the league.
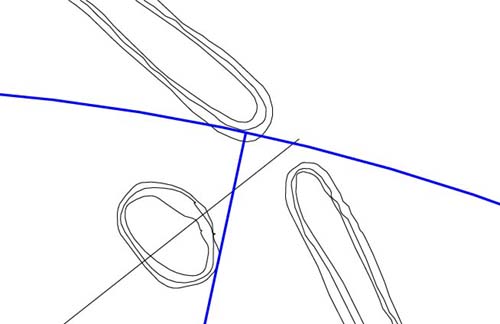
Figure 64: A very
vivid and easily identifiable code is displayed in the NE gateway. The vector
runs out 1296 feet from the horseshoe hub and, thereby, codes precession.
The diameter of this circle would equate to 2592 feet, with the number for
precession set at 25920-years. The azimuth angle of this vector is 12.15-degrees.
Note how it brushes the small mound en-route to its station.
- At Stonehenge, a region
of the outer face of the Heel stone sits 259.2 feet from site centre.
- At Silbury Hill in
Southern England the length up the diagonal face was coded to be 259.2 feet.
- The azimuth angle
of 12.15-degrees codes one of the foremost lunar numerical progressions, much
displayed at Stonehenge.
- At Stonehenge, both
solar and lunar cycles were counted out upon the 56-post positions of the
Aubrey Circle and the 6804-day lunar nutation cycle equates to 56 X 121.5
days or 28 periods of 243 days...hence the ancient tradition of 28 lunar mansions.
- The longest cross
measurement within the octagonal section of the Octagon complex is 1701 feet
and this distance is 1/4th of 6804. There are 140 increments of 12.15 feet
in 1701 feet.
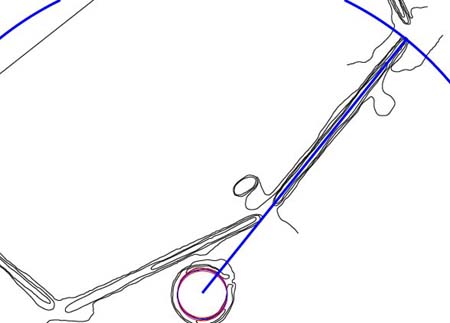
Figure 65: The horseshoe
hub anchored to the crest alignment of the ESE embankment, on an azimuth angle
of 38.88-degrees. The vector extending from the hub of the horseshoe runs
for 880 feet to the end of the ESE embankment, coding a very important increment
in the "11" series geodetic system.
- The length of 880
feet is 1/148500th of the ring of the Earth under the "11" series geodetic
system... Remember that one of the across site codes to the exterior positions
of the gateways was 1485 feet.
- As stated the angle
of 38.88-degrees is an increment in a precessional progression, based upon
12.96.
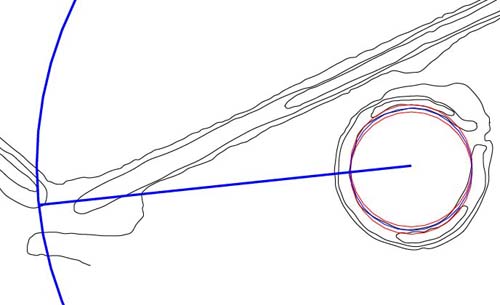
Figure 66: Another
vividly simple set of codes running from the horseshoe hub to the left side
of the southern gateway. The distance from the hub is 412.5 feet on an azimuth
angle of 264-degrees. In both distance and angle the coding is navigational.
- The distance of 412.5
feet is 1/40th of a league, 25 rods/ perches, 75 fathoms or 625 links.
- The azimuth of 264-degrees
codes a "mile" mathematical progression and the number 264 is conspicuously
displayed at Stonehenge, where the Station stones rectangle is 264 feet wide.
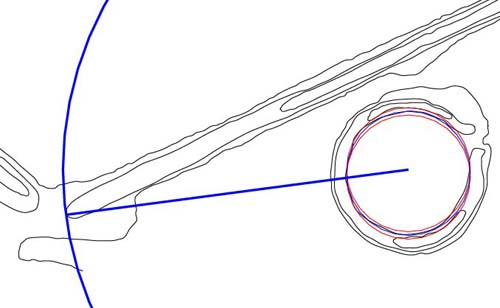
Figure 67: The ancient
astronomers attempted to code their important numbers as clearly as they could
and achieved an excellent result to the right side of the southern gateway.
The distance from the hub to the nose of the embankment is 375 feet on an
azimuth angle of 262.5 degrees. Incidentally, 375 is 1/7th of 2625. It's probable
that this distance was dual coded to also give a reading of 378 feet (1/2
the base length of the Great Pyramid).
- The 3.75 degree increment
is 1/3rd of 11.25-degrees, which is, in turn, 1/32nd of a 360-degree circle.
- The 262.5 number relates
to the reed measurement and 2.625 feet was 1/4th of a reed.
- The Serpent Mound
in Adam's County, Ohio is 525 feet from the tip of the tail to the apex extremity
forward of the head...which is 262.5 feet X 2...(also 50 reeds, 300 Celtic
Royal Cubits or 6300 inches).
- At Serpent Mound,
the azimuth angle from the tip of the tail to the pyramidal apex is 338.4-degrees
or 21.6-degrees short of true north. The 21.6-degree shortfall codes 2160,
which is the number of years it takes for the sun to move through one house
of the zodiac, as observed each vernal equinox. This value also codes the
diameter of the moon in miles.
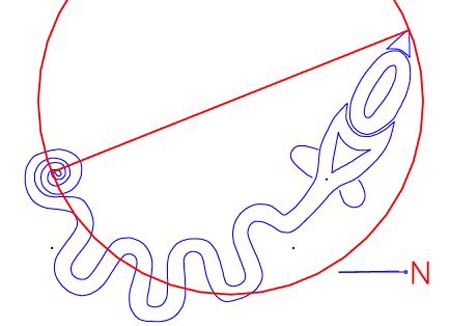
Figure 68: The Serpent
Mound of Adam's County, Ohio where many "Octagon-type", universal codes are
decipherable. The drawing depicted is based upon an AutoCAD reproduction of
mound researcher, William Romain's 1987 survey.
The foregoing gives a
cross section of codes found at stations across the Octagon site as they relate
to the hub position of the small horseshoe embankment. The sampling shown
is by no means complete and other stations, especially in the altar region,
can yet be identified.
In some rare instances there had to be minor rounding of numbers to add a
much sought after code.
For example, from the centre hub of the horseshoe to the centre hub of the
Octagon was 850.5 feet (315 rounded MY and also symbolically coding PI) on
an azimuth angle of 340.5-degrees.
Most assuredly, the number that the ancient astronomers wanted to achieve
in this azimuth was 340.2 (1/2 the duration of the lunar cycle was 3402 days...Khafre
Pyramid was 34020 inches in perimeter).
The constraints of exacting geometry, descending on a station from several
outlying positions, sometimes disallowed perfection and, in this instance,
the astronomers had to wear .3 of a degree of error in the code assignment.
The close proximity angle, however, continued to provide excellent mnemonic
reference to 3402.
We'll now turn our attention to secondary usages of the small horseshoe circle,
which related to solar or lunar rises and navigation.
TEACHING
INITIATES ABOUT SOLAR OR LUNAR RISE POSITIONS.
The small horseshoe circle
displays all of the attributes of a training centre, where the fundamentals
of how to work the greater site could be taught to apprentices.
From that position, the coded distances and angles to all other stations around
the site could be commented upon, with the significance of the numbers, as
well as their applications, fully explained.
The small horseshoe appears to be multifunctional in its potential applications,
where subtle reinterpretation of its anchor alignment to the ESE embankment
would allow for introducing added tutorials. We'll cover that aspect as we
proceed.
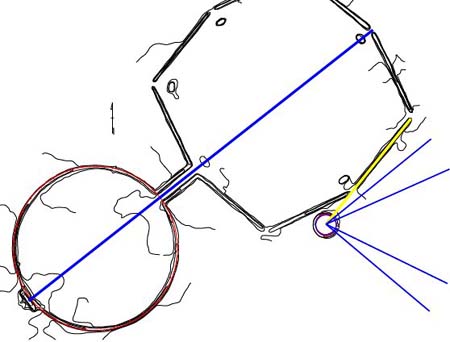
Figure 69: The blue
line extending through the full site represents a sighting line for viewing
the moonrise at major standstill. This is where the moon moves to its most
northerly position within the 18.613-year lunar nutation cycle. The viewable
horizon line, which was 30 minutes of arc (1/2 a degree) higher than the level
of the Octagon and 3.6 miles distant, meant that the moon rose within the
51.84-degree corridor, when the observer was situated atop the altar.
- A series of blue lines
are seen to extend out from the hub position of the horseshoe circle, whereas
an "anchor" line (yellow) ties the hub position to the 38.88-degree azimuth
of the ESE embankment.
- The blue lines represent
approximate northern and southern azimuth angles for the moon at major and
minor standstill, as seen from the centre of the horseshoe. The range for
major northern to major southern standstill is shown as 51 to 130-degrees.
The range for minor northern standstill to minor southern standstill is shown
as 66 to 116-degrees.
- The 66-degree azimuth
line extends out through the centre of the gateway of the horseshoe and this
minor northern standstill position of the moon provided an additional benchmark
for calibrations around the crest of the horseshoe.
- The true viewable
positions of rise for the moon depend upon the elevation of the distant horizon
and from the Octagon's altar the designated azimuth position was coded to
mean 51.84-degrees at major northern standstill. This occurrence, coupled
with this azimuth, represented the benchmark celestial event upon which the
site was founded, fixed and aligned.
- The horseshoe's "anchor"
line, along the crest of the ESE embankment, was at a known angle (38.88-degrees)
based upon 12.96-degree increases. Initiates learning the celestial arts from
the horseshoe hub location could calculate moonrise angles accordingly. The
centre of the gateway @ 66-degrees, provided an additional fixed angle.
Of course, very accurate
fixes for the lunar positions could be taken from the huge, main complex and
any lunar determinations made from the horseshoe were for training purposes
only. As we proceed, it will be demonstrated that the horseshoe circle is
merely a 1/10th ratio expression of the octagonal component that it sits adjacent
to and that the mathematical formulas of the larger structure are inherent
within the smaller.

Figure 70: Both the
yellow and blue lines are at known degree angles, which helped the astronomer/
teachers correctly calculate other degree angles. The 5 red lines give the
significant, albeit approximate, sunrise positions throughout the year, as
observable from the centre of the horseshoe.
- The topmost red line,
adjacent to the gateway, represents the approximate sunrise position at the
time of the Summer Solstice. This would have occurred at about 58-degrees.
Given that the horizon line was elevated marginally, the observable point
of rise was probably seen about 1/2 a degree further south, on the left edge
of the entryway embankment.
- The ancient people
of Europe held festivals at the midpoint period between solstices & equinoxes.
The second red line sits at 74-degrees and should describe that solar position
adequately.
- The 3rd red line represents
the position of the solar equinox and is designated as 90-degrees. As stated,
it would have made its appearance over the elevated horizon slightly further
south
due to the fact that it rises on a severe angle. The higher the horizon line
the further sideways the sun will move before it emerges into view.
- The 4th red line,
representing another interim period between equinox and solstice, extends
to an azimuth of 106-degrees.
- The 5th red line represents
the Winter Solstice position at approximately 122-degrees.
THE
DEEPER CODES OF THE HORSESHOE.
Masters of the craft,
teaching initiates how to read and work the greater Octagon site, needed an
"Octagon in miniature" from which to demonstrate principles of astronomy and
navigation.
Despite its meagre proportions, the horseshoe is quite complex mathematically,
to the extent that some of its attributes will go unmentioned in this preliminary
article.
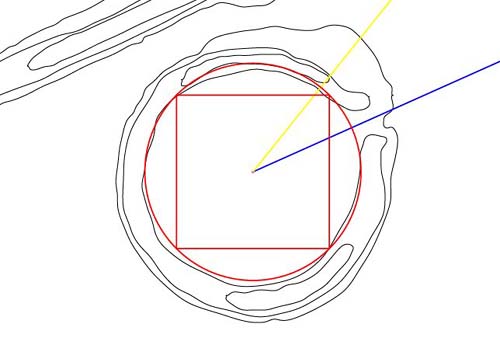
Figure 71: A case
of déja vue...the principles that led to the building of the octagonal
& circular embankments of the greater Octagon complex are being repeated in
miniature.
- The central square
has a radius of 47.25 feet, which makes it 1/10th of the size of the central
matrix square, running to 4 inner mound positions, within the Octagon. Note
how well the square fits on 3 out of 4 corner positions and how the circle
running to the corners of the square delineates the majority of the inner
embankment sweep.
- The horseshoe was
a place of intensive, concentrated coding and its meandering features, more
often than not, are present to demonstrate a length or angle code relating
to astronomy or navigation.
- The circle that encases
the 47.25 feet (Khafre height & lunar coded) radius square has a radius of
66.825 feet, which is exactly 1/8th of the size of the circle encasing the
Great Pyramid square in the Octagon's circle embankment. 534. 6 feet divided
by 8 = 66.825 feet.
Let's now add in the
1/2 PHI expanded squares, as found within the greater Octagon.

Figure 72: The 1st
of the 1/2 PHI expansions produces a square with a radius of 58.40421514 feet.
Note how it relates to large sections of the horseshoe, especially in the
eastern quadrant. The circle that encases this square has been marginally
reduced in size to 82.5 feet radius, and an error of 1.152 inches shortfall
exists between the rim of the circle and the corner of the square. The 82.5
feet radius is 1/2 of 165 feet (diameter), which codes the league measurement
of 16500 feet or the rod/ perch measurement, which was 16.5 feet.
We'll now complete the
initial series with the introduction of the final 1/2 PHI expanded square.
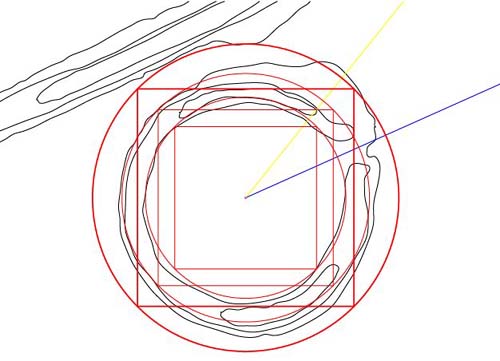
Figure 73: The final
1/2 PHI expanded square, for this preliminary series, is introduced. Note
how it extends to the outer limit of the left portal of the entryway. Note
also how the circle that encases it extends to the adjacent Octagon embankment
and how the Octagon's architects designed in a feature of additional outreaching
earthworks to accommodate this sweep.
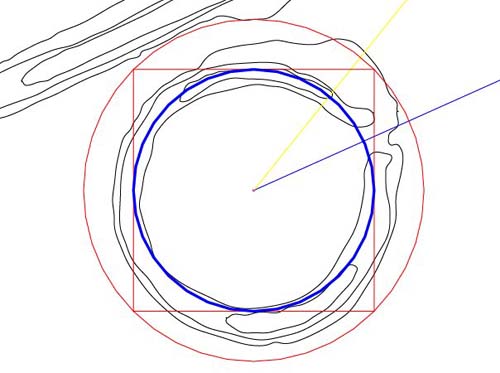
Figure 74: Whereas
the circle brushing the 72.19158405 feet (two 1/2 PHI expansions on 47.25
feet) square's corners extends to a main embankment, the blue circle contained
by the square was more important. It will be recalled that the main degree
angle calibration circle for the Octagon was 4536 feet in circumference, working
in conjunction with a double rendition of that circle @ 9072 feet. The blue
circle shown has a circumference of 453.6 feet (literally 453.5941609 feet
...453.6).
- The blue circle is
1/10th the size of the main calibration circle used within the Octagon for
identifying the exact position for the observation stations adjacent to each
gateway. Note how the blue circle interrelates with the curve of the southward
crescent atop the mound, as well as the inner embankment line of that quadrant.
- With the introduction
of a doubled version of the 453.6 feet circumference circle, centred on the
blue (66-degree azimuth) circle the observation methodology of the greater
Octagon could be duplicated and taught.
Let's return momentarily
to the PHI circles and squares before demonstrating the horseshoe's stellar
degree angle fixing method, as taught by the Masters of the Craft.
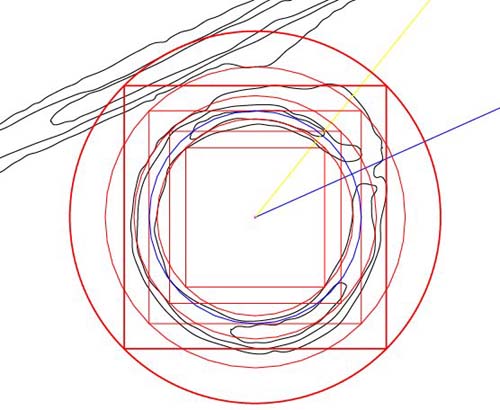
Figure 75: A final
square and circle, 1/2 PHI expanded over the preceding ones, extend onto a
main embankment. Relationships are readily seen in the way that the new circle
and square identify stations of the horseshoe or adjacent embankment. We'll
now rotate the squares onto the 66-degree line extending out of the entryway
to see further relationships.

Figure 76: The foregoing
is, in part, the design concept incorporated by the architects to shape the
horseshoe embankment circle... however, there's still a lot left in this compact,
code concentrated area to identify.
CONTINUE






























