Based upon the ancient edifice and landscape-structure evidence, scattered across the Eastern Mediterranean, Europe and throughout both North and South America, etc., these laboriously built Costa Rican monuments would have been fabricated to serve a very profound scientific purpose. Building this huge overland complex of mounds topped off with stone spheres and statues was no small undertaking, but required tremendous focus and commitment. The massive boulders, from which the precisely executed spheres were carved, had to be sourced from quarries found in the Talamanca range, 50-miles (75 kilometres) distant. Given Lothrop's calculation that some stones weighed in excess of 16 tons, the logistics of both carving and then transporting them to the pre-prepared mounds upon which they finally sat were horrendous. To say that logical humans would do this to "celebrate fertility" or some such trite purpose is pure bunkum.
To find out what purpose the vast, overland complex served, one has to delve into the root origins of this society, find out how it functioned and what its pressing day-to-day needs were ... such as establishing a working basis for the concept of "civilisation" and inter-cooperative national identity.

Another aspect of the overall evidence requiring careful consideration is the fact that many small stone balls were found in local graves as the former, prized possession of the deceased. What attribute of the ball necessitated its inclusion in the journey of the afterlife? A clue that will help answer this nagging question relates to the similar-inclusion of a round, disk-like Hypocephalus amulet in ancient Egyptian burials or of a highly geometrically incised pot in Beaker-people burials of ancient Britain.

To the left is seen an Egyptian Hypocephalus funerary object and to the right is seen a funerary beaker associated with the Neolithic Wessex or Beaker-people. These items accompanied the deceased in the journey of the afterlife.

The same lozenge design that adorned many funerary beaker pots was found upon golden lozenges worn by high priests of ancient British society. Egyptian and Hebrew-Phoenician priests also wore "breastplates" set out in geometric patterns, with the Hebrew-Phoenician ones sometimes referred to as "Urim & Thummin", meaning "light & truth.

Let's now consider a number of ancient cultural-religious attributes & practices, which impact equally upon Mediterranean-European and North-South American civilisations:

• The most ancient annuls and oral traditions of the British or many Continental European tribes speak of origins in the environs of Egypt and other countries of the Eastern Mediterranean. Physiological evidence derived from pre-dynastic and dynastic Caucasoid Egyptian mummies proves this as a statement of fact.
  
  
• Aspects of language, customs, cultural symbolism, gods, stories, musical instruments, mathematics, astronomical-navigational-chronology sciences, weights-measures-volumes, etc., have a provable pedigree back to Egypt. Even the venerable Oak tree worshiped by the European Druids came from that region.
  
  
• The Hypocephalus amulet of Egyptian funerary ritual was placed under the head of the deceased as a source of guidance. It's purpose was to provide all essential information in the perilous journey of the afterlife, wherein the newly dead had to travel for up to two years across the dark void of space to heaven (Orion ... where Osiris dwells). The path to heaven was fraught with many dangers and malevolent beings along the way, intent upon the destruction or enslavement of the traveler. It was only the knowledge contained within the Hypocephalus and the added use of potions or magic that would assure safe arrival at the destination.
  
  
• The panels of the Hypocephalus portray precise knowledge of astronomy and navigation. Featured centrally in the top panel is Ptah, the great architect of the universe and measurer of all things. He is seen holding his measuring square upon which the dog or fox traipses to the side. This denotes Sirius, the dog star or "pointer of the way" to Orion. The sideway's movement of Sirius refers to the Precession of the Equinoxes, as this binary star (the brightest in the night sky) was the primary target star for measuring Precession (as demonstrated at Stonehenge). The long central panel also denotes Precession, with baboons (the god Hapi) carrying the sun orb from one house of the zodiac to the next towards Amon-RA, the squatting Sun god (also pictorially represented in this way from North & South America to the Chatham Islands of New Zealand). The speckled baboons represent constellations and the pure white or albino one undoubtedly represents Sirius (the target for periodically measuring the rate of Precession).
  
  
• The traveler in the afterlife, armed with all of this wisdom, the accrued scientific knowledge of countless generations, was assured of staying on the path to heaven and not getting lost or led astray into outer-darkness and eternal captivity by monsters.
  
  
• The Wessex or beaker burial pots were adorned with the selfsame accrued scientific wisdom of the ages, as known to the high priests who kept order and maintained abundance in ancient British society ("the few set aside to bless the many"). The pots were symbolic repositories of navigational knowledge (externally), and other supplies (internally) for the journey of the afterlife. The great ancient navigators of the Pacific (the Lapita People) adorned their pots in the same way and, quite obviously, used the patterned and coded-design exteriors of the pots for mnemonic reference during long voyages. As a result of this navigational coding, Lapita pottery (dating to about 3000 BC) is found scattered across the vastness of the Pacific from Easter Island to New Guinea, a distance of over 6000-miles.
  
  
• The stone balls found on the landscape or in graves of Costa Rica are said, in age-old oral traditions, to represent the sun. The inference is that this is in similitude to the way that the sun is venerated on the Hypocephalus, with the sun-orb carried aloft by the baboon god Hapi, moving from one house of the zodiac to the next. Thousands of miles across the expanse of the Pacific Ocean, in New Zealand, many very ancient burials duplicated, in essence, the selfsame burial methods practiced by the ancient people of Costa Rica. Ancient people of New Zealand's South Island were buried in a trussed or sitting position with a huge round Moa egg accompanying the deceased into the afterlife. The Moa bird (now extinct) was a huge flightless bird, much larger than an Ostrich or Emu and the Moa egg in the burial seems to have carried the same "afterlife" religious significance as the Hypocephalus of Egypt, the round Beaker pot of Britain or the stone ball of Costa Rica.
  
  
• The Costa Rican balls were precisely fashioned in terms of diameter and circumference and in total represented many differing codes related to the sun, moon, planetary or stellar cycles and systems of navigation. The codes built into each orb came from an integrated mathematical parcel, shared between the highly mobilised cousin European nations. Each stone sphere, whether huge and immovable or small and portable, held a tutorial to be shared-around, compared with others and profoundly learnt by all. The orbs in the graves of Costa Rica represented (both symbolically and in terms of religious belief), a navigational aid to the deceased, in exactly the same way as the round Hypocephalus disk did to far-flung Egyptian cousins. All of the accrued scientific wisdom of this ancient society was imbued within the orb or within the dimensions and calibrations of an assortment of ancient stone disks found all over North and South America. Some of the "Mound-builder" stone disks, complete with their calibrated perimeters, date to perhaps 5000-years ago (3000 BC).

FARM 2, SECTION 40.

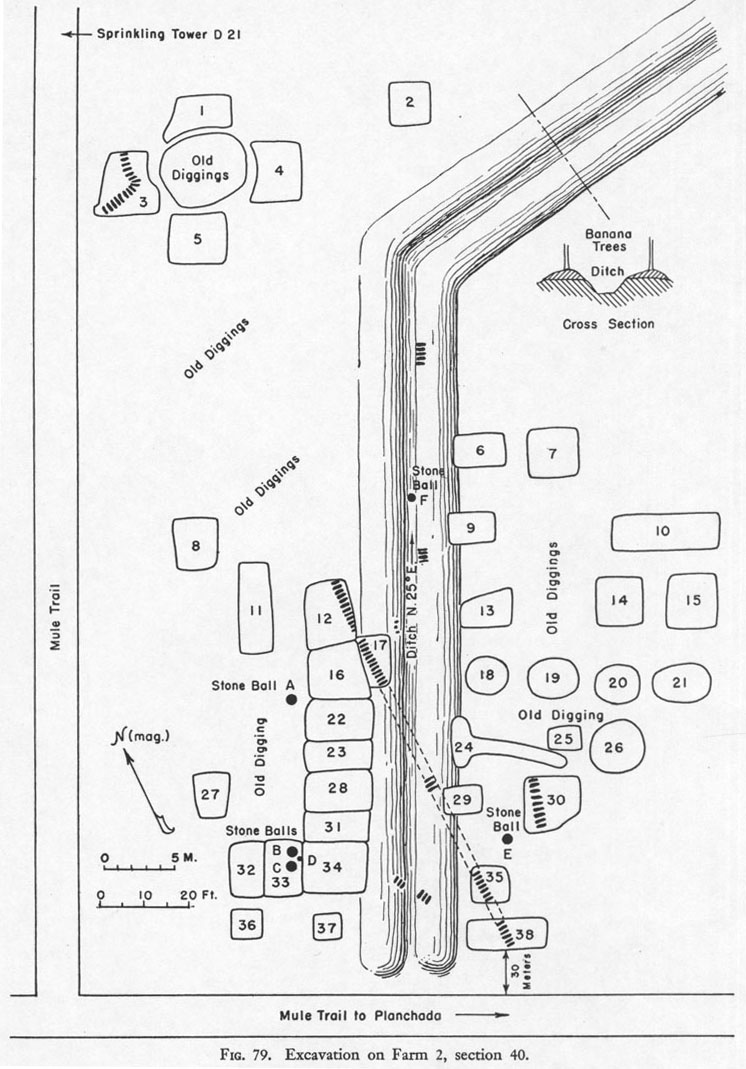
Lothrop's map of archaeological work done at Farm 2, Section 40. Again, the stone spheres encountered "in situ" are shown as black dots. A total of 6 were located in this section including a small stone ball "F", found in a ditch.

STONE SPHERE "A"

Lothrop measures this stone to have a diameter of 1.6666666-feet (1& 2/3rds) or 20-inches. One tutorial associated with this diameter is that in any 3,4,5 triangle the adjacent is 1.6666666 less in length than the hypotenuse.

The ancient mathematicians used several closely related variations on PI (3.1416) when seeking to have a perfectly calibrated circumference. The shortfall or excess in the true circumference was so small as to be visually undetectable. The most popular rendition of the PI ratio was 22/7ths (3.142857143); next there was the use of 314 & 2/11ths ÷ 100 (3.141818182); then there was 3.15 (3 & 3/20ths) and finally 3.125 (3 & 1/8th). Each form was used in particular types of calculation, wherein it was essential to have a perfect diameter produce a perfect circumference. In ancient navigation by the "6&7" family of numbers (the Greek mile of 5250-feet, etc.) linear distances covered (diameters) were converted to circumferences using the PI rendition of 22/7ths. When traveling according to the "11" family of numbers (the British mile of 5280 feet, etc.) linear distances were converted by the 3.141818182 rendition of PI.

The intended (tutorial related) circumference of Stone Sphere A was 5.25-feet or on half of a Hebrew Reed. This circumference is also 5 Greek feet. The symbolic conversion is done by the PI value of 3.15. Therefore: 1.66666666-feet X 3.15 = 5.25-feet. Based upon a true diameter of 1.66666666-feet the visible shortfall would be very close to 1/6th of an inch.

STONE SPHERE B.

The circumference of Stone Sphere B is 5.8333333-feet or 70-inches. This is the same division adopted by the ancient Swedish for their navigational "Famn", which was 1.2 Roman Paces of 58.3333333-inches each. Under the ancient Swedish system, which was perfectly aligned to the systems of both the Greeks and Romans, this circumference would also represent 2 "Steg" (fathoms) of 35-inches each or 3 "Aln" of 23.33333-inches each (23 & 1/3rd ... also called the "Rydaholmsalm"). It would also equate to 6 "Fot" of 11.666666-inches (11 & 2/3rds) each. Note: the ancient Swedish "Fot" was the same as the one used by the Romans, although the 11-inch "Fot" was also used by the Vikings and Germanic peoples of antiquity. All of the ancient cousin European nations derived their standards from the selfsame mathematical parcel, which had a pedigree back to Babylonian-Sumerian or Egyptian systems. All of the cousin nations used the full range of numerical options available for various kinds of calculations and pressed every number family into service for lunisolar-calendar or navigational computations.

Note: Given the average of all of Lothrop's measurements in different directions, another coded possibility is 5.76-feet of circumference or 69.12-inches (69 & 3/25ths). In a world calculated to be 12 X 12 X 12 X 12 X 1.2-miles in circumference (24883.2-miles ... The Great Pyramid Standard in Greek miles of 5250-feet each) the sum of 69.12-miles would be 1-degree of equatorial arc.

STONE SPHERE C.

Lothrop gives the circumference of this stone as 62.5-inches or 5.208333333-feet (5 & 5/24ths). This is a dynamic navigational mathematical progression associated with the "11" family of values and the mile of 5280-feet. There would be 1013.76 (1013 & 19/25ths) increments of 62.5-inches in a mile of 5280-feet. In a world considered to 24883.2 British Standard miles of equatorial circumference, 1-second of arc would be 101.376-feet and this is the exact width of the Parthenon of Athens' stybolite platform. A mathematical progression based upon 62.5 goes:

62.5, 125, 187.5, 250, 312.5 (note: there were 3.125-miles in the ancient British League), 375, 437.5, 500, etc.

Given some of Lothrop's other cross measures of this stone's circumference and the average derived there from, a value of 63-inches was also a distinct possibility as a secondary or symbolic code to be discussed in any tutorial associated with the stone's dimensions. The value "63" was one of the most prominent and dynamic of antiquity.

STONE SPHERE D.

Lothrop gives this circumference as 1.3333333-feet or 16-inches and a mathematical progression based upon "16" produces very important navigational numbers. Moreover, some ancient disk arefacts of Europe and the Americas are calibrated according to 32 or 320 circumference perimeter positions. Equally, a circumference of 16.2-inches would be dynamic. Using the form of PI @ 3.125 it would symbolically infer a diameter of 5.184-inches, which is a huge navigational and Precession of the Equinoxes code. The slope angle of the Great Pyramid is 51.84-degrees and the pyramid's base covers an area of 5184 square Hebrew Reeds of 10.5-feet each.

Also, if the value of 16.2 is divided by PI @ 22/7ths it equals a diameter of 5.1545454 (51 & 6/11 ÷ 10). This is 1/4th of the Egyptian Royal Cubit used in the construction of the Great Pyramid (756-feet ÷ 440 = 20.61818182). A Royal Cubit of this size is on display at the Turin Museum.

It's very likely that the Diquis Delta school of navigation provided many of these small balls, alongside the large ones, wherever lessons were being taught. Students could, therefore, have the opportunity to measure a wide variety of spheres and discuss the in-built codes and tutorials contained in each. Artefact evidence would suggest that a grouping of small spheres sat in a specially provided receptacle at this site, as a small tripod basin was found with sphere D.

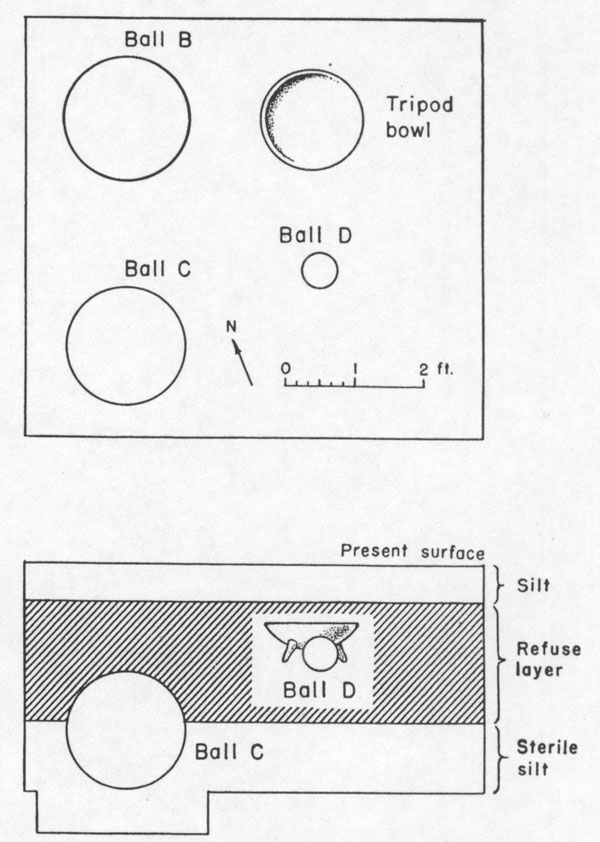
Lothrop mentions how 'the large tripod vessel perhaps may be associated with the balls'. It was found during an excavation alongside ball D. The diameter and circumference of this tripod vessel will also carry codes.

STONE SPHERE E.

Lothrop measured this ball to be 28.5-inches in circumference (2.375-feet). His average after measuring from various directions was very slightly higher. It would appear that the inbuilt code for this circumference was 28.512-inches. The same value was used as the basis for the Hebrew Sepphoris Dry Volume Measure.

HEBREW SEPPHORIS DRY VOLUME.

1 Homer….28512 cubic inches equals
10 Ephah….2851.20 cubic inches., or
30 Seah…..950.40 cubic inches, or
180 Cab….158.4 cubic inches, or
720 Log….39.6 cubic inches.

The 28512 number was a key to remembering 3 different navigational systems and working within them by simple manipulations of PI. Here's how stone sphere D worked:

1. 28.512-inches ÷ 22/7ths (3.142857143) = 9.072-inches. It just so happens that the Great Pyramid is 9072-inches (756-feet) long and , under that "6&7" navigational system, one side length of the Pyramid was 1/8th of 1-minute of Earth equatorial arc in a world that was 12 X 12 X 12 X 12 X 1.2 Greek miles (of 5250-feet each) in circumference.
   
   
2. 28.512-inches ÷ 3.141818182 = 9.075-inches. Under the "11" family of numbers one viewed the Great Pyramid as being 3-inches longer, with a side length of 9075-inches (756.25-feet) representing 1/8th of 1-minute of arc. For the "11" family system, the mile of 5280-feet was used and this equated to an Earth equatorial circumference of 24750-miles.
   
   
3. 28.512-inches ÷ 3.125 = 9.12384-inches. Although this "true size of the Earth" system was not easy to manipulate mathematically for navigation, it did tell the ancient people the "true equatorial circumference" to a tolerance of 18.8-miles, using very factorable numbers, reducible to an inch or less (actual size 24902-miles). Under this system the Earth was viewed as 24883.2-miles of 5280-feet in equatorial circumference. This is the system by which the Parthenon of Athens is built, with its platform being 101.376-feet wide or exactly the measurement for 1-second of equatorial arc.

STONE SPHERE F.

Lothrop measured this ball to be 19-inches in circumference. The true value would have been 19.008-inches and the code contained is simply a ratioed down expression of what's built into ball E. Therefore, 28.512-inches ÷ 19.008 = 1.5. In this case, however, the student of navigation learns how to remember the numerical combination to describe 1-minute of equatorial arc. Here's how ball F worked to the variations of PI:

1. 19.008-inches ÷ 22/7ths (3.142857143) = 6.048-inches. Under the Great Pyramids literal dimensions to describe the equatorial size of the Earth, two circumnavigations would be 6048-feet for 1-minute of arc.
   
   
2. 19.008-inches ÷ 3.141818182 = 6.050-inches. Under the second geodetic system that viewed the size of the Earth as 24750-miles, 1-minute of arc was 6050-feet.
   
   
3. 19.008 ÷ 3.125 = 6.08256-inches. Under the system that described the Earth as 24883.2-miles of 5280 feet each, 6082.56-feet was 1-minute of arc.

After years of being taught to the contrary, it might be difficult to conceive of the fact that these people were such adept mathematicians. All of the values expressed here (which are whole values and simple fractions that could be precisely derived or expressed with a manual abacus calculation device) are found within the dimensions and angles of ancient edifices and artefacts across several continents. They are also found to be present within all Weights, Measures and Volume Standards shared by the European cousin nations for thousands of years. In other words, we have undeniable evidence in structures or artefacts that these exact numbers were used and yet our mainstream "experts" teach that ancient civilisations did not achieve this level of mathematical competency.

Stone ball F was another of the very small ones that would have been placed within the tripod vessel on this site. Further archaeological probes around the immediate area would probably reveal several more.

Continue