A number value, derived from a measurement onto the Sarsen Circle's most elliptically extreme fascia to at least one of the outer circles, converts to a dynamic mathematical progression in the distance achieved. Let's look at a sampling of relationships to do with the station positions:
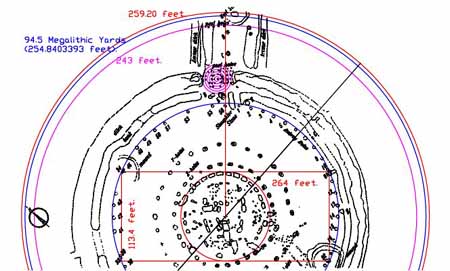
Figure 34: The length of the "station stones" rectangle is 264 feet and its width is 113.4 feet. Also shown is a circle, clearly marked by components, of 243 feet radius. Beyond that is another complying to 94.5 Megalithic Yards. Further out still is an extremity circle of 259.20 feet, which effectively sweeps the outer face of the Heel Stone. So what are some codes inferred in this sample?
(1). The 264 feet diameter of the station stone's rectangle is 132 feet X 2 and we have already seen many coded expressions of 132 at Stonehenge or the Giza Plateau of Egypt. This number is integral to the geodetic systems, which set distances to miles. The two long sides of the station stone's rectangle, under this "perfect" representation, add up to 528 feet. The British standard mile, with origins in Egypt, was 5280 feet.
(2). The 113.4 feet of width in this "perfect" rendition of the station stone positions is a very dynamic lunar code. It was used for determining time periods in the 6804 day lunar nutation cycle (60 X 113.4) or within the period of 16 lunar years, according to the Khafre Pyramid calibration...5670 days (50 X 113.4). The half value of 113.4 is 56.7. The base perimeter of Khafre Pyramid was 2835 feet...1/2 of 5670 feet.
(3). The 243 radius circle is a part of the lunar coding, with 243 months of 28 days each representing the 18.613-year (6804 day) nutation cycle. The numbers 243 or 113.4 were, therefore, used as septimal or sexagesimal breakdowns of 6804 days.
(4). If the 113.4 feet were read or adjusted to a PHI value of 42 Megalithic Yards (113.262373 feet) then this would be 1/4th of the Great Pyramid's literal height. Alternatively, 113.4 is 1/4th of the Great Pyramid's height under its sexagesimal assignment. As shown, Great Pyramid coding is strongly represented in component positions around the Stonehenge site, like in the clearly marked 189 MY diameter circle, which has an inch value of 6116.168142" (the Great Pyramid's PHI, face diagonal length, if it had a capstone, would have been 611.6168142 feet...226.8 MY...113.4 MY X 2).
(5). The distance from the face of the Sarsen Circle to the 48.6-degree rim of the 259.20 circle (brushing the Heel Stone) is 202.5 feet. This value is a lunar and rounded PHI, mathematical progression number, which produces numbers like 1620, 2430 & 4860.
(6). A 16.2 value exists in the difference between the 259.2 feet radius circle and the 243 feet radius circle (16.2 feet), again accentuating this important "rounded PHI" code. Remember also that 162-degrees featured as one of the "station stones" azimuth angles.
(7). Although the geometric method shown appears, strongly, to have constituted the benchmark and surveying approach taken for the initial layout of Stonehenge, it's possible that station stone 93 was manually adjusted to be 112 feet from station stone 94. In this way it could be used for recall of the "weights" system, which used both 16 (ounces) and 14 (pounds). The weight of 112 pounds was a hundredweight (cwt) and there were 20 cwt in a ton (2240 pounds). There were 22400 "rounded" PHI inches (1.62") in the perimeter circuit of the Great Pyramid (36288 inches)...a continuance of the Egyptian legacy, at Stonehenge, demonstrated yet again?
MAJOR & MINOR STANDSTILL OF THE MOON...RELATIVE TO THE STATION STONES.
Several authors have stated that the "station stones" positioning relates directly to major and minor standstill positions of the moon.
A comprehensive explanation of lunar movements will not be attempted here, as the moon follows a long, complex cycle that even reasonably adept astronomers have difficulty visualising and staying abreast of.
To partially explain major & minor standstill, let's quote author/ astronomer John Edwin Wood...'the moon swings each month from a maximum value of declination to a minimum value and back again...the amplitude of this oscillation will at some time be at its greatest, from about 29-degrees north of the celestial equator to 29-degrees south of the celestial equator...The time when the moon is swinging its farthest is called the major standstill, because the moon reaches about the same maximum height in the sky every month for something like three years. At the major standstill the moon's movements are at their most dramatic. Not only does it reach its highest possible elevation each month, but two weeks later it is very low in the sky, and barely rises in the high latitudes of the Shetland Islands.
These movements would have been very conspicuous to early man.
Just over 9 years after the major standstill, the moon's orbit has completed a full half turn and the monthly oscillation in declination will be much smaller: from about 19-degrees north of the celestial equator to 19-degrees south...At this time the moon is said to be at minor standstill, because once more it reaches approximately the same height in the sky for months on end.
From the observer's point of view its movements in the sky are far less dramatic than at the major standstill. Its maximum height in the sky is about 10-degrees lower at this time, and its minimum height is 10-degrees higher, so it does not show such a wide swing in its monthly movement (see, Sun Moon And Standing, pgs. 68-69...also Figs. 4.7, 4.8 & 4.10).
We'll now try to demonstrate the effect of the moon's major to minor standstills (rises and sets) as they relate visually to what's observable around Stonehenge's horizon.
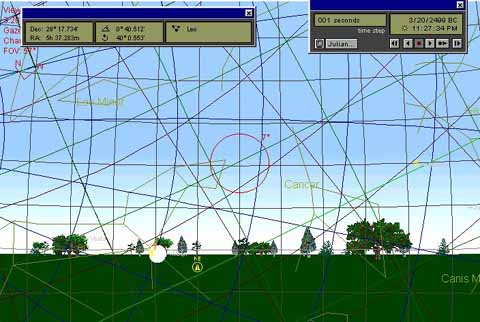
Figure 35: An alignment exists at Stonehenge, which would seem to indicate that the most northern point of observable "major standstill" rise of the moon was about 41-degrees. A set of posts mark an alignment at 40.5 degrees (to the left side of the posts), but one assumes a viewing corridor to "first glint" at the right of the posts (about 41-degrees). The white circle in the above picture indicates the moon close to observable rise (circa 2499BC) and a red cross near the top edge of the moon orb shows the horizon level, as seen from Stonehenge. The azimuth angle of 40.5-degrees contains a dynamic mathematical progression used for breakdowns of, primarily, the lunar numbers, 6804 days & 5670 days.
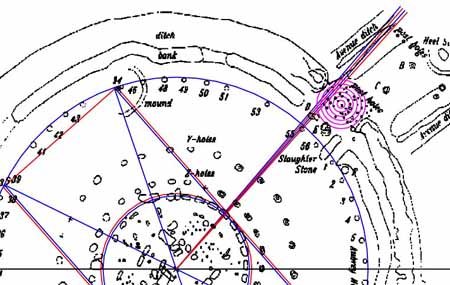
Figure 36: Ample scope existed in the Avenue post or circle calibrations to fix onto and track the northern-most rise position of the moon at major standstill. The top vector shown (blue) extends to the side of posts, set out along an azimuth of 40.5-degrees. Subsequent vectors clockwise increase in angle by 1/2 a degree, some falling to the side of post alignments or, in the case of full degree angle readings, to the edge-line of the concentric, Avenue calibration circles. All indicators would suggest that observing the northern major standstill rise position of the moon was of considerable importance to Stonehenge's astronomers.
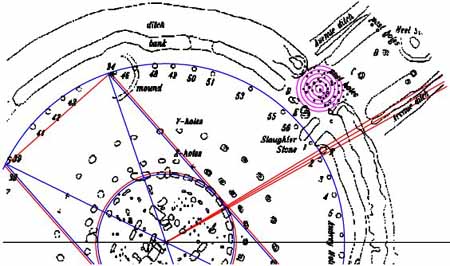
Figure 37: The 3 outrunning vectors (red) would converge upon the general position of the emerging and observable, northern minor standstill of the moon. The vectors shown run to 59, 60, & 61-degrees respectively. Given the slightly elevated, distant horizon beyond Stonehenge, the northern minor standstill was probably observed at about 60-degrees azimuth. This would seem to correspond to the Avenue ditch. A large alignment marker, adjacent to the Aubrey Circle, probably indicates the northern minor standstill of the moon to its right side.
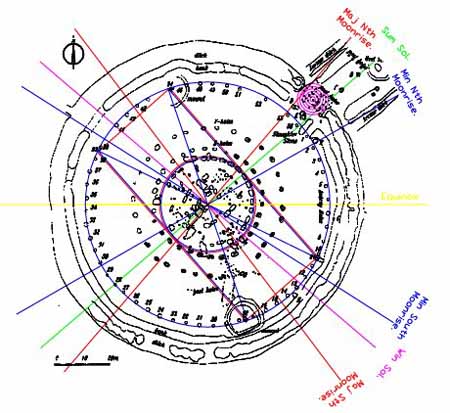
Figure 38: This picture should adequately describe the significant points of rise and set for both the sun & moon (circa 2500 BC). The labeled positions of rise are based upon calculated "first limb" appearances observable around the Stonehenge skyline horizon (see pgs. 570-572 of Stonehenge, Neolithic Man & The Cosmos, by Prof. John North). In his book, Prof. North gives the following readings on the height of the natural horizon: NE .6-degrees; E .65-degrees; SE .7-degrees; SW .6-degrees; W .45-degrees; NW .3-degrees.
Judging by the distribution of components or shaped features of the Stonehenge site, the positions of northern major standstill of the moon, summer solstice and northern minor standstill of the moon (Avenue region) were pre-eminent points of observation and clearly marked. The southern major & minor lunar positions and the winter solstice are, more conspicuously, marked at the points of set rather than rise, although one cannot discount the features of the southeastern natural horizon in providing distant "rise" outer markers for these events.
In summary, the station stones' positions work well in providing a corridor for southern major & minor lunar or winter solstice rises & sets. The survey benchmark azimuth, upon which the station stones rectangle is centred and 90-degrees opposed to, remains, most plausibly, 48.6-degrees. The northeastern side of the Heel Stone marks, with very good relative accuracy through many epochs, the mid-point between northern major & minor moonrise...(50.4-degrees).
THE 18.613 LUNAR NUTATION CYCLE & THE 5670-DAY (16 LUNAR YEAR) CALIBRATION
The four "station stones" were set out at Stonehenge to provide a corridor for the southern major/ minor standstill positions of moon (rise & set). It was also situated 90-degrees opposed to the summer solstice, with the summer sun acting as the primary surveying benchmark for the station stones orientation.
Working in conjunction with these marked positions were 56 posts on the Aubrey Circle, which acted as markers for counting, in days, the duration of both the 18.613 -year (solar years) nutation cycle of the moon, as well as 16 lunar years.
The lunar nutation cycle endured for 6798.32 days (ref. The Moon, by Zdenek Copal) but was calibrated, for mathematical breakdowns (progressions), through 6804 days. The period of 16 lunar years was calibrated to 5670 days.
Author/ astronomer, John Edwin Wood, in commenting on Hawkins's suggested method of counting the 56 post positions to predict the occurrence of eclipses adds, 'It has been criticised on the grounds that a large circle of holes is not needed simply for counting up to 56' (see Sun Moon And Standing, pg. 75).
What the critics overlook is that tangible, component based systems were always put in place, such that a forgotten principle could always be retrieved from the regional site or edifice. Whether or not the astronomers ever did manual counts on the Aubrey Circle posts or needed to refresh their memories by reference to its physical layout seems irrelevant...the circle was there primarily for mnemonic recall of the calendar and lunar cycle methods or as a teaching aid to apprentices of the astronomical arts.
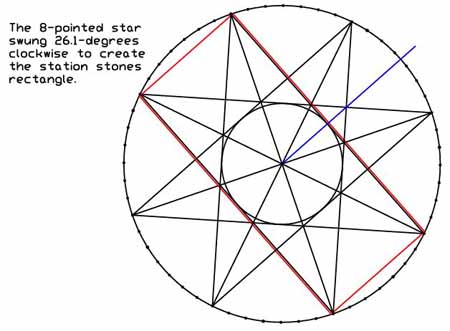
Figure 39: The red rectangle represents the 4-corner positions of Stonehenge's station stones, which were conceived by geometry within this 8-pointed star. The rectangle geometry was then marginally adjusted to provide 264 feet (geodetic code...2 sides 528 feet) and 113.4 feet (lunar code used to describe both the 6804-day nutation cycle, as well as the 5670-day, 16 lunar years period).
The circle in the centre is the PHI dimension (110 feet diameter of the Sarsen Circle, which was made slightly elliptical to code 113.4 feet between the Avenue (45-degrees azimuth) and Stonehenge's SW (225-degrees azimuth).
Calculating these two cycles could be done within the confines of the Aubrey Circle posts and between the rays of an 8-pointed star.
In one approach to doing the 6804-day count, the ray-points of the star had no value in providing numbers, but simply divided the circle into 8 parts, with 6 posts per part. Each of the 6 posts, between ray-points, was assigned a value of 141.75-days. This is a part of an important numerical progression which produces numbers found on the Khafre Pyramid (Egypt's Pyramid of the Moon)...141.74, 283.5 (Khafre's perimeter value was 2835 feet), 425.25, 567 (16 lunar years was 5670-days & the width of the station stone rectangle was 56.7 feet X 2), 708.75 (Khafre Pyramid was 708.75 feet per base side...2 X 354.375...the lunar year is 354.375-days long), 850.5, etc.
A second method could utilise all 56 positions and break the 6804-day period into 121.5-day period's (6804 ÷ 56). This method can be turned around to simply mean 243 months of 28-days duration each, between major standstills. Ancient "Lunarists" (those who calculated by the moon) used a "28 lunar mansions" methodology. Thus the 56 post positions (28 X 2) of the Aubrey Circle lend themselves admirably to the Lunarist modus operandi.
As far as the 5670-day (16-lunar year) period is concerned, it could also be calculated within the confines of an 8-pointed star, with each post representing 118.125-days. This is exactly 1/3rd of a lunar year or 4 lunar months of 29.53125-days duration each. Note also that the Khafre Pyramid base length was 708.75 feet, which was 29.53125 X 24 or 118.125 X 6. The degree of allowable error in the ancient lunar "mathematical progression" system was 57 seconds of excess time per lunar month.
One could also apply other types of calibration to these two periods (6804-days or 5670-days) as both were joined by ratio...6840 to 5670 is a ratio of 1.2 to 1.
Judging by the repetitive numbers occurring at Stonehenge or on Khafre Pyramid, it would seem that the count of 113.4-days was used to calibrate these two lunar periods...60 X 113.4 = 6804 & 50 X 113.4 = 5670. Remember that the station stone rectangle is 113.4 feet wide and the Sarsen Circle appears to have been made slightly elliptical to comply to a diameter of 113.4, from 45-degrees azimuth to 225-degrees azimuth.
The number 630 (which was the basis of the Greek Stadia...630 feet) and by consequence 105 or 10.5 (which became the basis of the reed measurement) were very important to the ancient people. With that in mind it's interesting to find that if the 56-post Aubrey circle is assigned a "beginning point" post and 180-degrees opposed, an "end point" post, then the whole lunar calibration can work very effectively within two halves of the Aubrey Circle through counts of 54 posts....27 per side.
6804 ÷ 54 = 126 (the ancient reed measurement was 126 inches). Alternatively, 5670 ÷ 54 =105 (the ancient reed measurement was 10.5 feet).
This system would allow for counts in increments of "reed type" values and in whole day numbers, simultaneously. For example: 6804 ÷ 630 = 10.8 (the Brasen Sea of the Temple of Solomon was 630 inches in circumference...the inner Sarsen Circle at Stonehenge was 315 feet...630 ( 2). Note also...one calibration of the Aubrey circle worked to 10800 inches (900 circumference feet X 12).
5670 ÷ 630 = 9...it's very easy to create suitable, easy to interpret calibration of these two lunar periods by utilisation of 54 posts (out of 56) for calibration...and the other two representing points of departure and termination.
The significance of a calibration set to 16 lunar years might seem elusive and of little practical usage. It is mentioned here solely on the basis that 56.7 occurs as a primarily important measurement code between components of Stonehenge. The numerical value had obvious importance to the ancient astronomer/ architects of the observatory and seems to have, accordingly, featured fairly prominently in lunar cycle determinations. Two circuits of the Khafre Pyramid, at 708.75 feet per side, were 5670 feet.
Researchers of the calibre of Hawkins, Hoyle, Colton & Martin have speculated that the eclipse cycle (Saros... 19 eclipse years...223 lunar months... 6585.32 days) could have been calculated using the 56 Aubrey Circle posts and have suggested various simple, plausible methods for doing so. Other cycles, such as the 19 solar years (235 lunar months...6939.69 days) Metonic cycle could also have featured within the wide range of calculations undertaken on and amidst the 56 Aubrey Circle posts.