USING THE NATURAL "V" IN THE LANDSCAPE TO TARGET MOUNTAINS TO THE ESE.
From the Waitapu standing stone observatory it can be seen that the long, distant Tutamoe Range tucks downward at a point about due east. At about the same location the end of Maunganui Bluff begins its upward ascent. The combination of these two natural features in the topography forms a "V" in the landscape, which was used from the Waitapu Observatory for getting a precise, "gun-sight" type degree angle fix.
The "V" was used as an alignment corridor to distant mountains. There are several marked examples of this, which are detectable in trig positions within the eastern and northeastern regions of the valley.
The most eastwardly apparent station using the declining ends of the Tutamoe Range and Maunganui Bluff hillside as a "V" sight onto a mountain is the field position where one observes the summer solstice sunrise occurring to the left edge of the tor mound.
Figure 22: This is the first possible occurrence of having a mountain nestled
in the "V". The trig from which this photo was taken also orientates
onto the rise position of the summer solstice sun. With good instrumentation
and a sound knowledge of the sun's rise attributes at the time of the solstice,
the southern most solar position (New Zealand summer solstice) could be translated
into a true overland angle onto the distant mountain's position. Regardless
of the difficulties encountered in making such complex angular determinations,
the fact remains that the ancient surveyors were positively using the "V"
as an alignment corridor onto mountains.
Let's wander up to the Bush-line solar observatory to see the same scene repeated.
Figure 23: One huge component stone of the Bush-line solar observatory,
long ago pushed from its pedestal and now lying forlornly in the encompassing
thicket of the forest. A component position associated with this observatory
sits 7680 feet from a marker on the the southern ridge tor mound of Maunganui
Bluff. The azimuth angle from this boulder cairn position to the tor marker
is 115.2-degrees. The 11.52 code is one of the biggest of antiquity. If one
doubles 1152 then it totals 2304…the same as if one triples 768. So in
both distance and angle the 1152, 2304 mathematical progression is being accentuated.
It's important to remember that the square footage value for a face of the Great
Pyramid was 230400 or that the Menkaure Pyramid was a total of 11.52 Egyptian
Pyramid acres of face and base area. These numbers were central to navigation
when using the "league" in linear distances covered or grid referencing
the Earth for successful traversal.
The angle back from a boulder marker on the tor mound to a "double stone"
position at the Bushline Observatory was 295.3125-degrees. This was in mnemonic
reference to the 29.53125-days in the lunar month.
Figure 24: From the hubstone of the Bush-line solar observatory
a mountain is vaguely recognisable through the morning mist. It sits nestled
in the "V". As we move further west and south the "V" becomes
more distinctive and its role as an alignment corridor is more visually apparent.
Figure 25: The view from a prominent, small standing stone circle on the
sea-cliff plateau above the Waitapu Observatory. Because of the elevation and
south-westerly position of this station away from the Bush-line Observatory
the "V" is more pronounced and, again, it has a far distant mountain
nestled perfectly within it, with yet other, closer mountains protruding above
the cairn marked ridgeline adjacent to the southern ridge tor mound.
By close observations taken from each marked position encountered throughout the region it become quickly apparent why cairns of boulder markers were placed precisely at those spots. Everywhere there is clear evidence of surveying and overland alignments onto far distant positions. People with a surveying background would readily see the very obvious signs of ancient alignment and overland distance mapping endeavours.
SO HOW DID THE ANCIENT SURVEYORS DETERMINE ELEVATIONS ABOVE SEA LEVEL?
Figure 26: On the southern side of the valley and at a chosen height of 960 feet above sea level the ancient surveyors modified the seaward cliff face and cut a horizontal ridge to act as a permanent benchmark for "height above sea level". This laboriously cut and shaped feature is arguably the most important single component created, which led on to extensive land mapping of the northern region of New Zealand. Immediately behind the horizontally cut ridge is an almost sheer drop to the sea. A measuring rope extending to the high or low water mark could quite easily divulge the exact chosen elevation for the cliff-face benchmark. Any necessary angling of the rope down the cliff-face to reach the sea, which led to a slightly distorted reading of height, could be calculated out by trigonometry. The height chosen was, without doubt, not arbitrary, but was a sought after useful number that could be fixed in memory. Special progressions of numbers based upon 6, 7, 11 or PHI were commonly used from ancient Egypt to Megalithic Britain, North America during the mound-building era and onward into Oceania.
Figure 27: The benchmark cleft is a shaped level feature that sits adjacent to fairly sheer cliffs and it is visible from many distant trig markers throughout the Waitapu Valley. In the photo left, taken with a telephoto lens, two seals are seen to be frolicking in the water at the base of the cliff 960 feet below the benchmark. The photo right shows the rear of the benchmark cleft and, beyond, the rising cliff-side terrain across the valley. On a lower substantial plateau is the complex, dual circle, Waitapu standing stone observatory. Behind the observatory on the rising hill slope are a series of carefully placed trig boulders, one of which is on a perfect level to the benchmark cleft.
The horizontal cut benchmark in the cliff-face was the first station of an
elongating and rising series of "surveyor's baselines" running north,
northeast and east that began with a line stretching for 2268 feet on a perfect
horizontal plane to its secondary station northward across the width of the
Waitapu Valley. The line resolved upon a trig stone situated above the standing
stone circle on the northern plateau.
Figure 28: The author (left) and Jeff Williams (right) out standing in their
field… by the trig boulder that is…, which sits 2268 feet across the
valley and on a level plane to the benchmark cleft. By careful observation of
the valley terrain it becomes glaringly obvious that boulders such as this were
brought to the location and precisely placed to fulfil a surveying purpose.
An optical instrument establishes that the boulder sits level with the benchmark
to the south. Jeff holds a recent model GPS (satellite navigational positioning
unit) to determine the boulder's latitude and longitude. The GPS was sufficiently
accurate for plotting the relative positions of about 100 structures scattered
over several square miles of terrain. With each attempt at plotting we generally
had 8-10 satellites passing overhead and indicated on the GPS screen, which
ensured that the fixes were accurate to within 6 or 10 feet.
|
|
The first baseline in the valley runs between the sea cliff benchmark
and this boulder at a known height above sea level. It also appears that
the target figure used by the ancient people for this baseline was 2268
feet, or the sum of 3 sides of the Great Pyramid of Egypt. The 2268 feet
figure is a special lunar code and represents 2268-days, which is 1/3rd
of the 6804-day lunar nutation cycle. The distance is also in a ratio of
1 to 1.25 of the distance around the Khafre Pyramid of the Giza Plateau
(2835-feet). Throughout this article the measurement standard used will be the ancient Egyptian, Sumerian, Babylonian standard, now known as The British Standard of Measurement. It was carried to Britain by the Neolithic Age and persisted there and in France since that time. After the Roman invasions several values of the original ancient measurements, such as the PHI based megalithic yard, "7" based reed or "11" based league were lost, fell into disuse or, like the "fathom" were modified (originally 5.5 feet). Ancient structures such as Stonehenge are positively and provably laid out according to this ancient standard, as are the structures of France, such as those of Rennes Le Chateau or Carnac. The GPS acquired distance close to 2268 (feet) suggests it was the mnemonic number chosen to represent the distance between the benchmark cleft and its 'cross valley, level trig boulder. |
Figure 29: The trig boulder 2268 feet north of and level to the shaped benchmark cleft in the seaward cliff.
WAYS OF CALIBRATING CIRCLES AND CYCLES IN ANTIQUTY.
As stated, "degree angle" system used by ancient New Zealanders was
the Egyptian/ Sumerian/ Babylonian sexagesimal angle system, based upon 360-degrees
of arc, with each degree breaking down into 60 minutes and each minute breaking
down into 60 seconds. A circle, therefore, was calibrated to be in, potentially,
1296000 parts, although it was not possible to visually detect 1 second of arc
on drawn circles.
By reference to Ptolemy's 13 volume"Almagest" (circa 140 AD) it would
seem that the Greeks, who had adopted the Babylonian circle calibration system,
were working to 7200 calibrations in a circle. This meant individual degrees
divided up into twenty parts each or down to 3 minutes of arc. The systems used,
either in circle calibration or daily time keeping, were numerical progressions
based upon the number "6".
The "full" choice of ancient circle calibration systems able to be
pressed into service also made provision for reading in increments of 630-degrees
of arc or in a numerical progression based upon the number "7" (septimal).
This second system was used for reading cycles within the calendar system. The
stadia measurement, (630 feet), which is based on the septimal reed, was adopted
by the fledgling Greek civilisation from the older, declining Egyptian civilisation.
Judging by how "one stadia" was marked into the running track at Olympia,
the length appears to have drifted into about 8 inches of excess error in 630
feet while in the possession of the Greeks. The Great Pyramid (3024 feet for
all 4 sides) is 4.8 Greek stadia (stadiums… of 630 feet each) in perimeter
value.
Another associated system that was popular in North & South America used
32 or 64 divisions of a circle. These alternative circle calibration systems
were not in conflict with the 360-degree system, but were simply added appendages
to it. The ancient people had at their disposal a wider range of increments
and choices than we traditionally use in modern times…all taken from the
same universal family and parcel of numbers.
To get some idea of how calendar cycles were working in numerical values and
progressions of 6, 7 or 8 see the article devoted to "The Calendar of
Coligny", within this website.
Based upon the 360-degree system, the azimuth angle from the benchmark cleft to the trig boulder, 2268 feet north, appears to have been coded to represent 345.6-degrees. This is a major navigational code and the outer rim circumference of the Sarsen Circle at Stonehenge, which was based upon PHI reductions of the Aubrey and "Y" Holes circles, was 345.6 feet. The Crosshouse (Temple of the Four Winds) at Miringa Te Kakara, near Bennydale, New Zealand, had a coded outer circumference of 172.8 feet (½ of 345.6 feet). The Great Pyramid was 1728 Royal Celtic Cubits, of 21 inches each, in perimeter value. These numbers were used profusely in ancient navigation under the sexagesimal/ septimal geodetic system. Mnemonic reference to the most used navigational method is encoded into the base dimensions of Silbury Hill in England, where a 550 feet diameter ("11" series) produces a 1728 feet circumference ("6" series), divisible by 360-degrees.
SO, WHAT'S A BASELINE AND WHY DID THE ANCIENT PEOPLE NEED ONE?
The ancient surveyors were involved in land mapping and needed to know how far away mountains, within line of sight from the Waitapu Observatory, were situated. They also needed to know the heights of those mountains. In order to accomplish this seemingly difficult task it was necessary to first establish two surveying stations separated by a known level distance and altitude. This first baseline was instrumental in creating other, longer and more elevated baselines, where 360-degree views were possible. For the best achievable accuracy in overland mapping it was necessary for baseline stations to be a "fair distance" from each other… the longer the better (within reasonable limits).
Once a long baseline was in place, hilltop-to-hilltop, the surveyor could go to each end of the line and take a very careful angle fix onto a target mountain. The baseline itself would run at a known true angle off north, south, east and west and all true angle assignments could have first been pre-determined by a "level plane" fix onto the equinoctial sunrise. Not surprisingly, the first valley baseline (2268 feet) runs across the Waitapu standing stone observatory, where a specific stone marks the position for observing the equinoctial sunrise twice a year on Tutamoe Range. Also a "V" formed by the declining end of the Tutamoe Range, conjuncting with the nearer declining end of Maunganui Bluff, provided a perfect easting. From that calculated fix correct degree angles could be precisely determined through 360-degrees of azimuth. Other prominent points around the skyline were at carefully worked out degree angles and could provide ongoing reference for any new azimuth fixes taken on celestial or terrestrial targets.
After taking angle fixes onto a common target from each end of a baseline one can either use trigonometry to determine how far away the mountain is or simply calculate it more manually. For example, if one used a long ruler that represented the whole baseline length in much reduced scale, then correctly angled measuring strings running from the ruler would indicate the "scaled" distance to the "target" (at the point where the strings intersected). The manual method could be easily and accurately accomplished in a flat field or on a long stretch of beach, where scaled baselines and the angles running from them could be marked on a flat surface of moist sand. Maunganui Bluff sits between such beaches, where nature has provided wide, flat and smooth markable surfaces.
Once the distance to the mountain has been established, then its elevation can be manually determined by the same simple method. All one needs is an angle upward from the point where the surveyor is situated to the peak or summit of the mountain. This is determined by use of a sighting stick with attached, calibrated protractor and plumb bob. The greater height value of the mountain is then added to the known height above sea level of the surveyor's position, from whence all fixes have been taken.
Sophisticated geometric evidence, based upon marked positions in and beyond the Waitapu Valley, shows that trigonometric calculations were undertaken and that the surveyors were not limited to "manual" means only in establishing surveying positions. It's quite feasible to conclude that surveyors issuing forth from the ancient schools of learning had the capacity to memorise a sufficient number of sine, tangent and cosine ratio values to accomplish all tasks down to a refined value of ¼ of a degree of arc or less (which was visually detectable). One would not be obliged to memorise all such values through 360-degrees of arc…only sufficient to cover angles related to one quadrant or "quarter of the Earth". The numbers could also be positively recorded on a string knot "kupu"…also known as a "quipu" in South America.
Creating sets of accurate baselines that linked the high hills to each other
at precisely known distances was "no mean feat" and required very
careful surveying work. Some baseline stations were invisible from their "twin"
station and positions were laboriously calculated by the placement of interim
trigs, from which the final end station position could be established.
This preliminary, level baseline of 2268 feet, at an azimuth angle of 345.6-degrees
from the benchmark, was the first in a series that then "stepped"
the original baseline upward to, ultimately, the highest achievable levels on
both sides of the valley. After much precise work and calculation, a whole series
of level or near level baselines of known length and elevation existed throughout
the valley. These extended, where practicable, on level planes to marked positions
near or onto the highest points. In most cases the final positions afforded
360-degree views onto the distant mountains or landmarks across the country.
Because of the fact that the endpoints of all Waitapu Valley baselines were
of known "level length" (even if a perfectly level baseline was unachievable
hilltop-to-hilltop), precise angle calculations could be done from the carefully
marked baseline end point trigs to determine distances to all mountain summits
or hill crowns within 360-degrees of vista, as well as their elevations above
sea level.
It goes without saying that after the tremendous effort undertaken to create
the multi-component surveying system within the valley, the final precisely
calculated base line lengths and angles had to be positively remembered, and
that information handed on intact to ensuing generations. For this reason every
effort was made to ensure that a final baseline length was founded upon a highly
recognisable number. Because the ancient parcel of repetitive and significant
astronomical/ navigational numbers was relatively large, small adjustments and
manipulation in the design and subsequent setting out of trigs or tor mounds
could ensure that baselines were set to very recognisable distance codes and
angles.
The first valley baseline heading northward seems to have incorporated 960 feet
of elevation, 345.6-degrees (navigation) of azimuth angle from the benchmark
to its level trig and 2268 feet (lunar & navigational code) of distance.
By use of coded numbers and angles from the universal parcel (originating in Egypt), remembering the valley baseline system was relatively easy. Such well understood numbers and angles greatly facilitated the surveying calculations that followed. It might prove very significant that Maori have a tradition handed down from ancient times of venerating particular boulders or outcrops and calling them (with deep respect) by names. Close analysis of those names might denote or hold clues as to the nature of an individual alignment and the length it represented, just as the name PI means 3.1416 to us or PHI means 1.6180339. There was an interval in time when newly arriving Polynesian and Melanesian Maori lived peaceably with the earlier groups and gleaned much information from them.
HOW FAR AWAY IS THAT MOUNTAIN?
To find out the ratios that existed between the sides of any right angled triangle
(tangent, sine and cosine) all the ancient people needed to do was draw a wide
variety of triangles, of differing hypotenuse slopes, (down on a beach?*) and
then back engineer each triangle to extract the ratio values between side lengths.
These ratio values, for differing angles, could then be recorded by knots on
a quipu string and used in all future surveying applications where the selfsame
degree angles occurred. In the final analysis, it was only the sine value or
ratio of the "opposite" over the "hypotenuse" that needed
to be recorded or fixed in memory and known. These values or ratios needed to
be known for all triangles with slope angles from 0-degrees to 90-degrees at
increasing, visually detectable increments for overland sightings…say increases
of .25 of a degree or 15-minutes of arc.
Theoretically, these values could be stored on a "quipu" (kupu) string-knot
mnemonic device.
In seeking to find a fully manual method for working out how to use the Waitapu Valley baselines to calculate the distance to outlying mountains I asked my son, Gene, to "dream up a scenario" wherein only sine needed to be used. He quickly devised the following method. Given that the ancient people could dwell on and contemplate solutions to mathematical problems over decades of time, they would have devised exceptionally fluid and simple systems for very complex calculations
The formula for finding the distance to any outlying mountain from a Waitapu Valley baseline (assuming a baseline in this instance of 8000 feet) is the following:
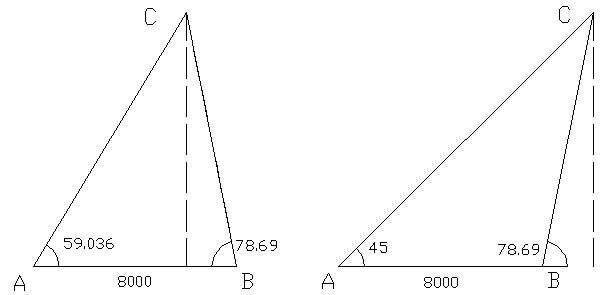
Figure 30: Two hypothetical situations are shown of attempting to determine the distance to a mountain (point C) from a Waitapu Valley baseline of 8000 feet length. Such a baseline runs between the two tor mounds on opposite sides of the valley. The first scenario assumes a target that falls within the limits of the baseline (within a quadrant or 90-degrees of arc…viewing out to one quarter of the Earth). The second scenario assumes a need to calculate a distance slightly beyond the quadrant (viewing into another quarter of the Earth). (Gene Doutré).
This exercise shows one method of solving the triangulation problem by a manual approach. It was certainly within the capacity of the ancient mathematicians to devise such systems.
Out of interest, there might prove to be a link between the ancient use of the term SIN or Syne (the 21st letter of the Hebrew Alphabet), which found its way into both French or English usage, and Christianity's usage of the term SIN. The term SINE has long been used to describe curves, chords and arcs and it was probably an important word to the Druids, who maintained a direct link to the Hebrew Phoenician traders. Perhaps, along with so many other symbols or concepts of so-called Paganism, SINE suffered the indignity of degenerating into SIN in church-speak… to describe evil and wrong doing… for which one needed to repent. The Christians certainly had a great distaste for Pagan geometry and did all that they could to eradicate it or ban its use.
*Footnote: If the ancient mathematicians of the Waitapu Valley wished to experiment with a wide variety of right-angled triangles to extract sine, tangent and cosine ratios between sides, then creating the triangles would have been easy. In the building industry we use 3,4,5 triangulation to "square" up building lines, also known as the 3,4,5 squaring method. On such perfectly squared triangles the adjacent is "3", the opposite is "4" and the hypotenuse is "5". This exact system of triangulation (3,4,5) was used to create the Khafre Pyramid of Egypt. The dimensions of that pyramid positively demonstrate the principles of the 3,4,5 triangle, with half the base length being 354.375 feet (adjacent), the height being 472.5 feet (opposite) and the diagonal side length being 590.625 feet (hypotenuse). These dimensions relate to the lunar cycle (year) and are based upon an increment of 4 lunar months (118.125-days) X 3, 4 or 5. At Maunganui Bluff, with locally accessible, expansive beach surfaces providing hard, washed and smooth drawing surfaces, differing slope angles could be assigned to a drawn 3,4,5 triangle and the ratio variations recorded. It wouldn't take very long to gain and record a dossier of ratio values that could be used in all future surveying work.