THE GREAT PYRAMID, KHAFRE & MENKAURE PYRAMID GEOMETRY ENCODED INTO THE NEW ZEALAND LANDSCAPE.

There are a multitude of theories concerning the purposes of the Great Pyramid, as well as those of Khafre and Menkaure Pyramids of the Giza Plateau. Whatever the more extended and speculative possibilities were, the edifices worked perfectly to serve the function of a World Bureau of Standards for astronomical cycles, navigation, weights, measures and volumes principles. It would seem that cousin peoples, travelling from pre-dynastic Egypt to set up colonies on other continents, religiously preserved the knowledge encoded into the pyramids by marking it into their newly discovered and settled landscapes. This profound "out of Egypt" knowledge had to be remembered at all cost, as to lose it was to lose one's grasp on the concept of mobilised, optimised and fully functioning civilisation.

Dimensions and angles of the 3 pyramids of Giza, both internally and externally, code a highly sophisticated and scientific system of metrology in use at a very early epoch. The coffers of each pyramid were, undoubtedly, for housing measuring rods, volume vessels and weights. These were the world's master standard sets, kept in perfect temperature-controlled environments that never varied, summer to winter, day or night.

Ancient emissaries from distant lands could return to Egypt as commissioned representatives of their people to periodically check their nation's weights measures and volumes standards against the master set. New, precisely fashioned sets could also be issued to satellite or more isolated cousin nations and, regardless of certain national, popular preferences related to a weight, measure or volume increment, all standards used were tied to a common origin.

Moreover, all weights and volumes used by individual nations coded some aspect of the lunar cycle or navigational (Earth size) knowledge, etc. Measuring rods used by the cousin peoples were largely the same or simple ratio increases and decreases on the length most preferred by another nation. In order to facilitate trade and the exchange of resources, each system being used regionally was in a fluid, easily calculable ratio relationship to those used in other cousin nations. This standardisation persisted in the Mediterranean and Europe reasonably intact until a fairly late period of the Roman era.

It can be shown that the measurement systems worked very well and in ratio to each other if based upon the British Standard inch. The same holds true in the ratios existing between volume measures. Weight systems, which were originally determined by counting out and weighing, mainly, wheat grains (the origin of the term "grains" as a unit of weight) were also in a perfect ratio to each other between nations. Because of these workable relationships in ancient metrology the British Standard of Measurement can be shown to be as old as the pyramids themselves.

SO WHO WERE THE "COUSIN PEOPLES" THAT DESCENDED FROM THE PYRAMID BUILDERS?

If we analyse the features of pre-dynastic Egyptian or Sumerian skeletons, then the physical anthropology shows a skeletal type consistent with that found in Swiss cist graves, the London plague pits or the tumulus mounds of Europe. The craniological evidence of pre-dynastic Egyptian or Sumerian skeletons alone shows the long faces of European Caucasoid skull types. Egypt and Mesopotamia were, amongst several other countries in the Middle East and Near East, European homelands before a mass exodus from those increasingly parched territories in about 5000-4000 BC.

The waymark trails composed of cairns and standing stones from this early era exodus were still very much in evidence in the late 1800's. They extended from Israel along the North African coast to the Pillars of Hercules across from Gibraltar, then from Spain to France and Scandinavia. Another set of waymark trails ran to China and Korea.
Despite present academic opinions to the contrary, the pyramids were already steeped in age by 5000 BC, with the possible exception of Menkaure Pyramid, which was abandoned by its builders to the encroaching aridity before it was fully completed.

As these former Egyptian/ Sumerians (to use generalised umbrella terminology) found new homelands around the world on many continents, they encoded their profound pyramid knowledge into the landscape of the colonial territories, such that it could never be lost.

These early, nomadic cousin peoples were known by a multitude of names in various epochs and their migratory history and pedigree is well known in certain historical circles, based upon well-founded oral traditions, cultural idiosyncracies and documented evidence.
For convenience, some authors commenting on the latter era European amalgamations of such groups will refer to them as "pre-Celts" rather than their more specific names of Fomorians, Firbolgs, Tuatha De Danann, Milesians, Britons, etc. Regardless of the umbrella terms used to describe them in various epochs and locations, these cousin peoples set up colonies worldwide in remote antiquity, including the country of New Zealand at the base of the South Pacific.

At much later eras several other ethnicities had settlements in New Zealand, as evidenced by oral traditions, cultural symbolism or introduced flora originating on other continents…as well as skeletons reposing in New Zealand burial caves.

PYRAMID GEOMETRY.

Two-dimensional representations of the Great Pyramid are found in the geometry of Stonehenge in England, as well as that of the Octagon of Newark, Ohio in North America. Unsurprisingly, Great Pyramid, Khafre and Menkaure two-dimensional geometric representations are found carefully marked into the landscape of the Waitapu Valley region of New Zealand as well.

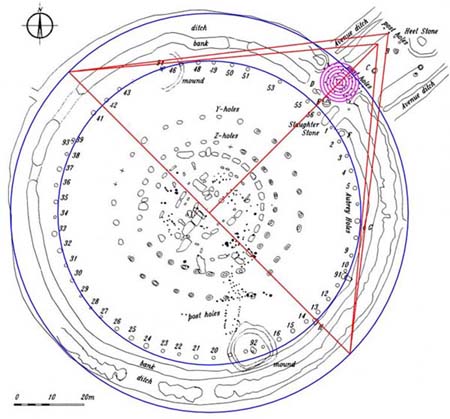
Figure 1: The Stonehenge site was built to be slightly elliptical, but it can be seen that a circle of 378 feet diameter perfectly houses the Stonehenge site from 45-degrees azimuth to 225-degrees azimuth. The diameter of that circle is precisely ½ of the length of the Great Pyramid. A line running through site centre from 135-degrees to 315-degrees forms the base of a ½ scale Great Pyramid and a stone sitting adjacent to the Aubrey Circle (marked "H") helps to establish that line. A perfect ½ scale replica of the pyramid is then drawn, with side slopes equating to 51.84-degrees. The front face of a post on the Avenue marks the position where the two converging lines intersect at the apex.
The actual Great Pyramid, however, always had a flat top and it was essential that it did in order for it to demonstrate specialised "circumference of the Earth" codes based upon the pyramid's vertical height. In the above picture lines brushing the Aubrey Circle posts determine where the "flat top" altar floor of the Great Pyramid commenced.
The two-dimensional geometry of the Great Pyramid is clearly marked into the Stonehenge site…Let's now see how it was (along with the configurations of Khafre and Menkaure Pyramids) carefully marked into the New Zealand landscape half a world away from Stonehenge.

Figure 2: Four yellow circles appear on this map, which are the locations of some of the most important and laboriously created structures of the Waitapu Valley region. Apart from providing stations from which many coded alignments commenced, the primary function of these four sites was to preserve knowledge of the dimensions and angles of the pyramids of the Giza Plateau.

SITE 1.

Figure 3: A laboriously cut stone feature in the sea cliff provided a benchmark position, at a known height above sea level, for determining overland elevations. The right hand picture (depicting the back side and top level ridge of the Benchmark Cleft in the foreground) shows a view up the coast toward the much-modified coastal hill, which is situated about 1.8 miles from this starting position.

This is the Benchmark Cleft on the seaward cliff and it represents ground zero for a giant 3,4,5 triangle. The triangle itself is based upon a "half Khafre Pyramid" profile. The 3,4,5 triangle line (opposite) runs up the coastline for 9450 feet (20 X the height of Khafre Pyramid @ 472.5 feet). The line resolves upon a much-modified seaward hill then turns 90-degrees (adjacent) that runs for 7087.5 feet (half the base length of Khafre X 20) to the Kerr Road Observatory. The line then turns to form the equivalent of Khafre Pyramid's side or slope angle, which is 53.13010235-degrees (the angle of all 3,4,5 triangles) and runs for 11812.5 feet (the face length of Khafre X 20) to reconnect at ground zero on the Benchmark Cleft.

SITE 2.

Figure 4: This picture falls far short in describing the steepness of the coastal hill. Position 1 relates to a series of boulder cairns, standing stone markers and a small tor mound behind the tree. Position 2 is the saddle of the hill, which has two assembly plateaus at slightly differing elevations. Position 3 is the summit, with several sighting pits set into terraces and adjacent marker stones. Position 4 has many cut, level terraces facing north, which are very effective for casting shadows with the rising and setting sun. This set of 26+ shadow clefts becomes very prominent around the time of the summer solstice. A very nice, double hump tor mound sits on the ridge behind trees in the left side of the above picture.

This is a highly modified and very high hill at the end of the seaward range. Its base drops to near sea level and rises steeply for just over 680 feet to a fairly compact summit plateau. It's evident that this hill was a major junction for alignments and overland surveying activities, as it has several sighting pits, large boulder cairns, assembly plateaus, shadow clefts, standing stone markers and a very nice ridge tor mound, which is situated slightly south of the summit.

SITE 3.

Figure 5: The central stand of large obelisks in a line at the Kerr Road Observatory, all now lying with the tops to the east. This is a very important junction site, with many individual markers, such as boulder cairns or standing stone circles and sighting pits, dotting the plateau. Much work remains in taking positional fixes on individual marker clusters and analysing their unique purposes.

The "slightly below ridge" aspect of the main central obelisks negates their use for visual orientations toward the east or northeast, although there is a clear view to markers on Puketapu Hill northward. One can safely surmise that the laboriously erected, giant obelisk boulders had to be exactly at that prescribed position to fulfil some very important design purpose within the seaward sector of view. By merely moving them a short distance east they could have sat on an elevated ridge, with almost 360-degrees of vista.

SITE 4.

After seeing pyramid geometry strongly suggested in the Maunganui Bluff regional landscape and testing GPS coordinates in AutoCAD, it became evident that a specifically placed marker would, undoubtedly, exist on the northern ridge of the Waitapu Valley. The geometry encountered seemed to suggest that a marker was essential to set up a geometric association between the other 3 points. I duly back-calculated the GPS coordinates to fix the exact position of this marker before visiting the location on the 5th of October 2002. The marker in question, if it existed, would be in deep bush. When approaching the approximate location, I read out the coordinates to research colleague, Sid, who entered them into the GPS. We then followed the unit's arrow pointer to the prescribed position, where it began spinning to indicate ground zero. The sought after solitary marker turned out to be a pile of 9 very large, purpose placed boulders that were situated on the skyline and would once have been clearly visible from the other 3 locations. These boulders could well have been erected as a pillar at the time of initial construction. Nearby we found an intriguing small glade clearing, some peripheral cairns (one substantial) and some single standing stone markers. Although we explored the forest extensively further east, no further markers were encountered.

Figure 6: This is one of 9 large marker boulders in a heap, the location of which was first determined by calculation, then verified by an expedition up onto a forested ridge to the predicted coordinate position. If the vast, overland, 2-dimensional, pyramid geometry theory was to be validated, then the boulder pillar had to reside exactly at this spot.

CONTINUE